Programmation de la méthode

Christophe Prud'homme <christophe.prudhomme@cemosis.fr>, Laurent Navoret

Gmsh

Gmsh (logiciel libre): https://gmsh.info

Création de maillage élément finis \(2 \mathrm{D} / 3 \mathrm{D}\)
Interface graphique

différentes versions (version 2 / version 4 )

Exemple

Créer un fichier carre. geo

// parametres
h =0.2;
L =1;
// Definition des points: stem:[(x, y, z)] et taille de l'element /
Point (1)={0,0,0,h};
Point (2)={L,0,0,h};
Point (3)={L,L,0,h};
Point (4)={0,L,0,h};
// Definition des lignes
Line (1)={1,2};
Line (2)={2,3};
Line (3)={3,4};
Line (4)={4,1};
// Definition de la surface
Line Loop (5)={1,2,3,4} ;
Plane Surface (10)={5};
Physical Line ("Dirichlet")={1,2,3,4};
Physical Surface ("Omega")={10};

Exemple

commande pour générer le fichier .geo

gmsh carre.geo

Pour générer le maillage : Mesh / 2D
Pour générer le fichier gmsh : File / Save mesh
Pour changer la couleur: Tools / General / Color / Predefined color scheme / Dark
Pour afficher le numéro des noeuds: Tools / Mesh / Visibility / Node Iabels
Pour afficher le numéro des éléments \(2 \mathrm{D}\) : Tools / Mesh / Visibility / 2D element Iabels
Création d’un fichier msh en ligne de commande:

gmsh -2 -order 1 carre.geo -o carre.msh

Fichier .msh

$MeshFormat
4 0 8
$EndMeshFormat
$Entities
4 4 1 0
1 0 0 0 0 0 0 0 // Point 1
2 1 0 0 1 0 0 0 // Point 2
3 1 1 0 1 1 0 0 // Point 3
4 0 1 0 0 1 0 0 // Point 4
1 0 0 0 1 0 0 0 2 1 -2 // Line 1 entre Point 1 et Point 2
2 1 0 0 1 1 0 0 2 2 -3 // Line 2 entre Point 2 et Point 3
3 0 1 0 1 1 0 0 2 3 -4 // Line 3 ...
4 0 0 0 0 1 0 0 2 4 -1 // Line 4 ...
1 0 0 0 1 1 0 1 1 4 1 2 3 4 // Line 5
$EndEntities

Fichier .msh

$Nodes
9 45
1 0 0 1 // Point 1
1 0 0 0
2 0 0 1 // Point 2
2 1 0 0
3 0 0 1 // Point 3
3 1 1 0
4 0 0 1 // Point 4
4 0 1 0
1 1 0 4 // Line 1
5 0.1999999999995579 0 0
6 0.3999999999989749 0 0
7 0.5999999999989468 0 0
8 0.7999999999994734 0 0
2 1 0 4 // Line 2
9 1 0.1999999999995579 0
10 1 0.3999999999989749 0
11 1 0.5999999999989468 0
12 1 0.7999999999994734 0
3 1 0 4 // Line 3
13 0.7999999999999998 1 0
14 0.6000000000013869 1 0
15 0.4000000000016644 1 0
16 0.2000000000008322 1 0
4 1 0 4 // Line 4
17 0 0.7999999999999998 0
18 0 0.6000000000013869 0
19 0 0.4000000000016644 0
20 0 0.2000000000008322 0
1 2 0 25 // Surface 1
21 0.7124999999991418 0.7124999999993721 0
22 0.7125000000000453 0.2875000000003787 0
.....
$EndNodes

Fichier .msh (fin)

$Elements
1 68
1 2 2 68 // 68 triangles
1 21 43 29 // triangle 1 avec noeuds 21 , 43 et 29
2 29 43 33
3 41 29 35
....
$EndElements

vient de Physical Surface(1) = {1};
sans cette instruction : toutes les Elementary entities sont décrites
pour marquer les bords, on peut ajouter dans le code .geo

Physical Line (11) = {1 ,3};
Physical Line (12) = {2 ,4};

Autres commandes

Maillage triangulaire structuré

Transfinite surface {1};

Maillage quadrangulaire

Recombine surface {1};

Maillage 3D par extrusion

Extrude {0 ,1. ,1.5}{ Surface {1}; Layers {3}; Recombine ;}

Assemblage de la matrice

\[\begin{aligned} A_{i, j} &=\int_{\Omega} \nabla \varphi_{i} \cdot \nabla \varphi_{j} \\ &=\sum_{K \subset \operatorname{supp} \varphi_{i} \cap \operatorname{supp} \varphi_{j}} \int_{K} \nabla \varphi_{i} \cdot \nabla \varphi_{j} \\ &=\sum_{K \subset \operatorname{supp} \varphi_{i} \cap \operatorname{supp} \varphi_{j}} \int_{K} \nabla \psi_{K, \hat{\imath}} \cdot \nabla \psi_{K, \hat{\jmath}} \end{aligned}\]

La plupart des intégrales sont nulles par construction, il suffit alors de parcourir les éléments \(K\) du maillage et de rajouter les contribution sur chaque élément à la matrice \(A\) grâce à la propriété d’aditivité de l’intégrale.

Matrice de connectivité:

La paire \((K,\hat{\imath})\) fournit la numérotation locale de la fonction de base et \(i\) la numérotation globale. La relation entre les deux numérotation est donnée par la matrice de connectivité ou table des dégrés de liberté

\[\mbox{connect}\left(\text {ind}_{K}, \hat{\imath}\right)=i\]

le couple de fonctions de base \(\psi_{K,\hat{\imath}}, \psi_{K, \hat{\jmath}}\) contribue au terme \(A_{i, j}\) avec \(i=\mbox{connect}\left(\text {ind}_{K}, \hat{\imath}\right)\) et \(j=\mbox{connect}\left(\text {ind}_{K}, \hat{\jmath}\right)\)
principe de l’assemblage : calculer les termes \(\int_{K} \nabla \psi_{K, \hat{\imath}} \cdot \nabla \psi_{K, \hat{\jmath}}\) et les ajouter au fur et à mesure dans la matrice.

Assemblage de la matrice

Rappel: Changement de variable \(T: V \rightarrow U\) un \(C^{1}\) difféomorphisme
\[\int_{U} f(x) d x=\int_{V} f(T(y))|\operatorname{det}(\nabla T(y))| d y\]
Calcul des coefficients: \[\int_{K} \nabla \psi_{K, \hat{\imath}} \cdot \nabla \psi_{K, \hat{\imath}}=\int_{\hat{K}} \nabla \psi_{K, \hat{\jmath}}\left(T_{K}(y)\right) \cdot \nabla \psi_{K, \hat{\jmath}}\left(T_{K}(y)\right)\left|\operatorname{det}\left(\nabla T_{K}(x)\right)\right| d y\]

avec \(i=\mbox{connect}(K,\hat{\imath})\), \(j=\mbox{connect}(K,\hat{\jmath})\);

Assemblage de la matrice

Proposition: \[\nabla \psi_{K, \hat{\imath}}\left(T_{K}(y)\right)=\nabla \hat{\psi}_{\hat{\imath}} \nabla T_{K}(y)^{-T}\]

On a \(\psi_{K, \hat{\imath}}(x)=\hat{\psi}_{\hat{\imath}}\left(T_{K}^{-1}(x)\right)\) donc \(\nabla \psi_{\hat{\imath}}(x)=\nabla \hat{\psi}_{\hat{\imath}}\left(T_{K}^{-1}(x)\right) \nabla T_{K}^{-T}(x)\) puis \(\nabla \psi_{\hat{\imath}}\left(T_{K}(y)\right)=\nabla \hat{\psi}_{\hat{\imath}}(y) \nabla T_{K}^{-T}\left(T_{K}(y)\right) .\) Puis \(\nabla T_{K}^{-T}\left(T_{K}(y)\right) \nabla T_{K}(y)=I d\)

Si \(T_{K} \text { affine } \Rightarrow \nabla T_{K}(y) \text { matrice constante (indép. de } x\)

Les Formules de quadratures sont construites sur \(\hat{K}\)

Transformation géométrique

\[\hat{X} = (\hat{x}_0,\ldots,\hat{x}_{d-1})^T : \mbox{point dans} \hat{K} \subset \mathbb{R}^d\\ \hat{X}_i = (\hat{x}_{i,0},\ldots,\hat{x}_{i,d-1})^T: \mbox{ sommets de } \hat{K}\\ X_i = (x_{i,0},\ldots,x_{i,d-1})^T = T_K(\hat{X}_i), \quad i=1 \ldots d+1 \mbox{ sommets de K}\\ X = (x_{0},\ldots,x_{d-1})^T = T_K(\hat{X}), \quad \mbox{point de K}\\ \psi_i \mbox{ ieme fonction de base de Lagrange sur } \hat{K} \mbox{ associée à } \hat{x}_i\\ x_j = T_K(\hat{x})_j = \sum_{i=1}^{d+1} x_{i,j} \psi_i(\hat{x}), \quad j=0\ldots d-1\\ \hat{\nabla} T_K(\hat{x}) = (\hat{\nabla} T_K (\hat{x})_0, \ldots, \hat{\nabla} T_K (\hat{x})_{d-1} ) \quad \mbox{ indep de } \hat{x}\\ \mbox{calcul } |\mathrm{det} \nabla T_K |, \quad \mbox{calcul } \nabla T_K ^{-1}\\\]

Formule de quadrature

Definition: Soit \(K\) polygone et \(n \in \mathbb{N}^{*} .\) On considère

\[Q(\phi)=\sum_{i=1}^{n} \omega_{i} \phi\left(\xi_{i}\right) \quad \approx \int_{K} \phi(x) d x\]

\(\left(\xi_{i}\right) \in K^{n}:\) points de quadrature
\(\left(\omega_{i}\right) \in \mathbb{R}^{n}:\) poids de quadrature

Ordre de quadrature

C’est le plus grand entier \(m \in \mathbb{N}\) tel que l’intégrale soit exacte sur \(\mathbb{P}_{m}\)

Estimation d’erreur: \(\exists c>0\) telle que \(\forall \phi \in C^{m+1}(K)\)

\[\left|\sum_{i=1}^{n} \omega_{i} \phi\left(\xi_{i}\right)-\int_{K} \phi(x) d x\right| \leqslant c \operatorname{mes}(K) h_{K}^{m+1}\|\phi\|_{C^{m+1}(K)}\]

\(\operatorname{mes}(K):=\) volume de \(K\)

Formule de quadrature

Cas du simplexe dans \(\mathbb{R}^{2}: \hat{K}=\left\{x, y \in \mathbb{R}_{+}^{2}, \quad x+y \leqslant 1\right\}\)

Coordonnées barycentriques: \(A_{1}=(0,0), A_{2}=(1,0), A_{3}=(0,1)\)

\[(x, y)=\lambda_{1}(x, y) A_{1}+\lambda_{2}(x, y) A_{2}+\lambda_{3}(x, y) A_{3}\]

avec \(\lambda_{1}(x, y)=1-(x+y), \lambda_{2}(x, y)=x, \lambda_{3}(x, y)=y\)

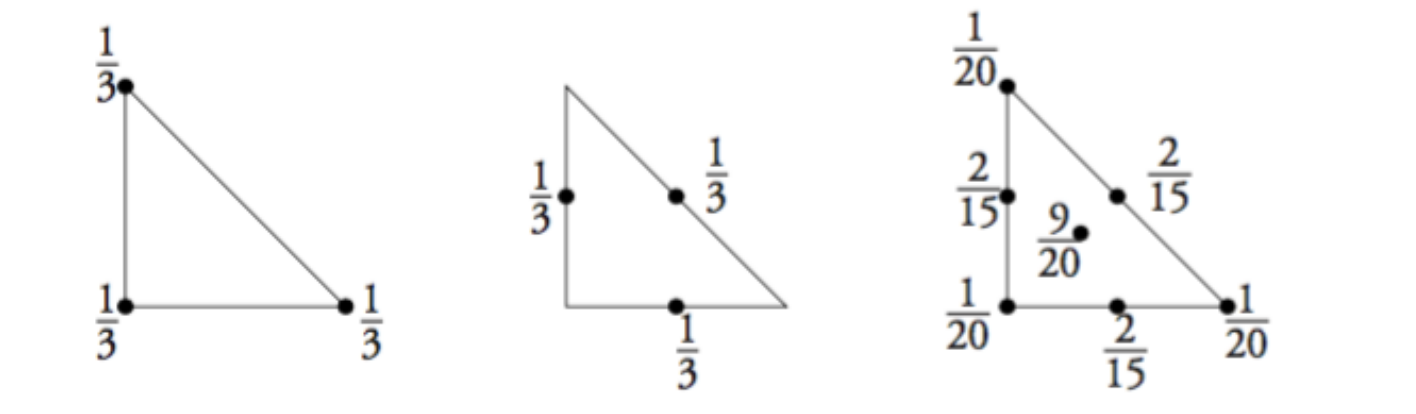
Formule de quadrature

Table 1. Exemples de quadratures, \(S=\operatorname{mes}(\hat{K})=1 / 2\)
\(n\)	ordre	coord. barycentrique	multiplicité	poids
3	1	\((1,0,0)\)	3	\(1 / 3 \times S\)
3	2	\((1 / 2,1 / 2,0)\)	3	\(1 / 3 \times S\)
7	3	\((1 / 3,1 / 3,1 / 3)\)	1	\(9 / 20 \times S\)
		\((1 / 2,1 / 2,0)\)	3	\(2 / 15 \times S\)
		\((1,0,0)\)	3	\(1 / 20 \times S\)

Multiplicité

Definition: Dans le tableau précédent, nous appelons multiplicité le nombre de permutations qui doivent être effectuées sur les coordonnées barycentriques pour obtenir la liste de tous les points de la quadrature.
Exemple: La formule du premier ordre comporte 3 points ; les coordonnées barycentriques et les poids correspondants sont

\[\{1,1,0;1 / 3 \times S \}, \{0,1,1;1 / 3 \times S \}, \{1,0,1;1 / 3 \times S \}\]

Algorithme d’assemblage

Données: on stocke les poids de quadrature dans un tableau poids. On stocke les valeurs des fonctions de formes et de son gradient aux points de quadrature dans les tableaux psi et derpsi.

# Boucle sur les elements
for ik in range ( Nel ):
    compute ( detTK )
    compute ( nabla_TK -1)
    # Boucle sur les points de quadrature
    for l in range ( nq ):
        # Boucle sur les fonctions de formes
        for ni in range ( nk ):
            i = connect (ik , ni )
            for nj in range ( nk ):
                j = connect (ik , nj )
                derpsii = derpsi [ ni ,l ] * nabla_TK -1
                derpsij = derpsi [ nj ,l ] * nabla_TK -1
                A[i ,j] += detTK * poids [l ] * derpsii @ derpsij

Même algorithme pour le calcul du second membre.

Conditions de Dirichlet

Conditions de type Dirichlet: fonctions de bases associés aux noeuds des bords à retirer

En pratique, pour ne pas modifier la taille de la matrice en fonction des conditions aux limites, on assemble la matrice avec tous les noeuds y compris ceux du bord

Méthode d’élimination
Méthode de pénalisation
Méthode de Nitsche, voir les explication ici

Méthode d’élimination

on modifie les lignes associés aux noeuds du bord. On met les lignes à 0 sauf 1 sur la diagonale et la valeur de la condition au second membre. On écrit simplement ce que valent les degré de liberté aux bords Dirichlet.

Afin d’avoir une matrice symétrique on peut aussi modifier les colonnes correspondantes et le second membre. Cependant ce n’est pas nécessaire de le faire, le gradient conjugué, par exemple, n’est pas impacté par cette modification(on peut le montrer).

Méthode de pénalisation

on modifie la matrice avec \(\varepsilon> 0\) ainsi

\[\begin{array}{l} A_{i, i} \leftarrow A_{i, i}+\frac{1}{\varepsilon} \\ f_{i} \leftarrow f_{i}+\frac{1}{\varepsilon} g_{i} \end{array}\]

Discussions

Algorithme élimination

for i in dir_nodes:
    # acces ligne i de la matrice A et du vecteur F
    A[i,:] = 0  #mettre `a zero la ligne correspondant
    A[i,i] = 1 # 1 sur la diagonale de la matrice
    F[i] = 10 # mettre la valeur de la solution

avec ce code u[i] = 10, i in dir_nodes.

Deux facons de faire pour le calcul de la norme \(L^2\) et de la norme \(H^1\):

calcul des intégrales directement
calcul via les matrices

Norme \(L^2\)

Ppur une fonction \(u_h\) dans un espace élément fini

\[\| u_h = \sum u_i \phi_i \|_2^2 =\int_\Omega u_h*u_h \approx \\ \sum_K \sum_{q=1}^Q w_q u_h \circ T_K (\hat{x}_q)*u_h \circ T_K (\hat{x}_q) |det \nabla T_K | \\ u_h\circ T_K (\hat{x}_q)= \sum_{i=1}^3 u_{connect(K,i)} \phi_i(\hat{x_q})\]

choisir une formule de quadrature d’ordre \(2k\) pour \(u_h \in P^k_{c,h}\)

Norme \(L^2\) (suite)

Pour une fonction \(u\) qui n’est pas dans un espace élément fini, on a:

\[\|u \|_2^2 =\int_\Omega u*u \approx,\quad \sum_K \sum_{q=1}^Q w_q u \circ T_K (\hat{x}_q)*u \circ T_K (\hat{x}_q) |det \nabla T_K | \\\]

il faut calculer \(x_{K,q}=T_K(\hat{x}_q)\), puis calculer \(u(x_{K,q})\).

SemiNorme \(H^1\)

\[\|\nabla u_h = \sum u_i \nabla \phi_i \|^2_2 =\int_\Omega \nabla u_h \cdot \nabla u_h = \\ \sum_K \int_\hat{K} \nabla u_h \circ T_K \cdot \nabla u_h \circ T_K |det \nabla T_K | = \\ \sum_K \int_\hat{K} \hat{\nabla} u_h \nabla T_{K}^{-T} \cdot \hat{\nabla} u_h \nabla T_{K}^{-T} |det \nabla T_K | \approx \\ \sum_K \sum_{q=1}^Q w_q \hat{\nabla} u_h \nabla T_{K}^{-T} * \hat{\nabla} u_h \nabla T_{K}^{-T} |det \nabla T_K | \\ \hat{\nabla} u_h = \sum_{i=1}^3 u_{connect(K,i)} \hat{\nabla} \phi_i,\quad \nabla u_{h_|K} = \sum_{i=1}^3 u_{connect(K,i)} \hat{\nabla} \phi_i \nabla T_{K}^{-T}\]

SemiNorme \(H^1\) (suite)

Si \(u\) quelconque, soit on calcule l’interpolant de \(u\), \(\pi^1_h u\), dans \(P^1_{c,h}\) puis la semi norme \(H^1\) en utilisant l’interpolant, soit on connait le gradient de \(u\) et on utilise celui ci dans les formules de quadratures

\[\pi^1_h u (x_j) = \sum_{i=1}^N u(x_j) \psi_i(x_j) = u(x_j) * \delta_{i,j} = u(x_j)\\\]

\(\pi^1_h u \) est l’élément de \(P^1_{c,h}\) dont les composantes sont \((u(x_1),\ldots,u(x_N)))^T\).

 # nodes renvoit une paire (i,(x,y))
for N in nodes:
    Piu[N.i] = fonction_u(N.x,N.y)

Assemblage des matrices de raideur

\(A\) avec condition de dirichlet.

on assemble \(A\) sans condition Dirichlet.

\[\|\nabla u_h \|^2 = U_h^T A U_h = \int_\Omega \nabla u_h \cdot \nabla u_h\\ u_h = \sum_{i=1} U_i \psi_i(x)\]

avec \(U_h\) le vecteur des composantes de \(u_h\) dans la base de Lagrange \(P^1\).

Assemblage des matrices de raideur (suite)

Pour \(u\) on a

\[\|\nabla u \|^2 \approx \|\nabla \pi^1_h u \|^2 = \Pi_h^T A \Pi_h = \int_\Omega \nabla \pi^1_h u \cdot \nabla \pi^1_h u,\quad \mbox{ avec } \pi^1_h u = \sum_{i=1} u(x_i) \psi_i(x)\]

avec \(\Pi_h\) le vecteur des composantes de \(\pi^1_h u\) dans la base de Lagrange \(P^1\).