Elasticité Linéaire

Christophe Prud'homme <christophe.prudhomme@cemosis.fr>, Laurent Navoret

Problème d’élasticité linéaire

\[\begin{array}{rl} \nabla \cdot \sigma(u)+f&=0 \mbox{ sur } \Omega\\ \sigma(u)&=\mu\left(\nabla u+\nabla u^{T}\right)+\lambda(\nabla \cdot u) \mathrm{Id}\\ u&=0 \mbox{ sur } \partial \Omega_{D}\\ \sigma(u) \cdot n&=h \mbox{ sur } \partial \Omega_{N} \end{array}\]

  • \(u: \Omega \rightarrow \mathbb{R}^{d}:\) champ de déplacement

  • \(\sigma(u) \in M_{d}(\mathbb{R}):\) tenseur des contraintes

  • \(\lambda, \mu>0:\) coefficients de Lamé du matériau

  • \(f: \Omega \rightarrow \mathbb{R}^{d}\) force volumique

Elasticité linéaire

Petites Déformations

  • \(\varepsilon(u)=\frac{1}{2}\left(\nabla u+\nabla u^{T}\right):\) tenseur des déformations

  • \(\nabla \cdot u=\operatorname{tr}(\varepsilon(u))\)

  • \(\rightarrow \sigma\) dépend linéairement de \(\varepsilon(u)\)

Version intégrale
\[\forall \omega \subset \Omega, \quad \int_{\partial \omega} \sigma(u) n=-\int_{\omega} f\]

Forces surfaciques

\(\sigma(u) n\)

représente une densité de force surfacique (\(N/m^2\)) dont la normale unitaire est \(n\)

\(\int_{\partial \Omega_N} \sigma(u) n\)

représente la force (\(N\)) s’appliquant sur le bord \(\partial \Omega\).

Matériau hyperélastique

Pour de nombreux matériaux, les modèles élastiques linéaires ne décrivent pas avec précision le comportement observé du matériau. L’exemple le plus courant de ce type de matériau est le caoutchouc, dont la relation contrainte-déformation peut être définie comme non linéairement élastique, isotrope, incompressible et généralement indépendante de la vitesse de déformation. L’hyperélasticité fournit un moyen de modéliser le comportement contrainte-déformation de ces matériaux.

Le modèle de matériau hyperélastique le plus simple est le modèle de Saint Venant-Kirchhoff qui n’est qu’une extension du modèle de matériau élastique géométriquement linéaire au régime géométriquement non linéaire.

Matériau hyperélastique de type Saint Venant-Kirchhoff
\[\varepsilon(u)=\frac{1}{2}\left(\nabla u+\nabla u^{T} + (\nabla u)^T \cdot\nabla u \right)\]

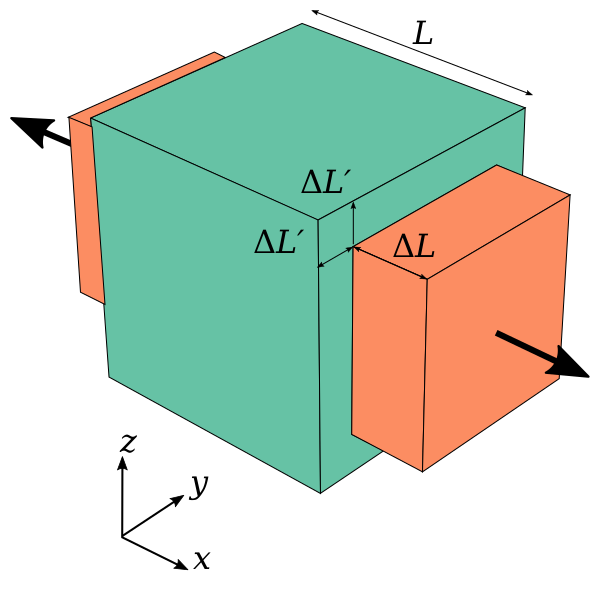
Coefficient de Poisson \(\nu\) et module de Young \(E\) (en \(3\mathrm{d}\))

Interprétation

\[E=\frac{\mu(3 \lambda+2 \mu)}{\lambda+\mu}, \quad \nu=\frac{\lambda}{2(\lambda+\mu)}\]

Si on effectue une élongation verticale d’une longueur \(\varepsilon\) alors:

  • la contrainte de traction à opérer est de l’ordre de \(E \varepsilon\)

  • la compression horizontale, relativement à \(\varepsilon\) est de l’ordre du coefficient de Poisson

    Unités

  • \(E\): En unités de base SI : \(Pa = kg m^{-1} s^{-2}\); Dimension : \(M L^{-1} T^{-2}\)

  • \(\nu\): sans dimension \( 0 < \nu \leq 0.5\), \(\nu=0.5\) matériau incompressible

Interprétation

En effet, en considérant le champ de déplacement suivant pour un cube:

\[u=\left[\begin{array}{c} -\nu \varepsilon x \\ -\nu \varepsilon y \\ \varepsilon z \end{array}\right]\]

le tenseur des contraintes associé \(\sigma\) est solution du problème avec

  • \(0=\sigma_{11}=\sigma_{22}\) (contrainte normale nulle sur les bords horizontaux) et

  • \(\sigma_{33}=E \varepsilon(\text { contrainte normale sur le bord du haut })\)

  • \(\rightarrow\) Grand \(E=\) matériau rigide, faible \(E=\) matériau souple

poisson ratio wikipedia

Analyse vectorielle

champs de vecteurs et de matrices

  • \(u=\left(u_{1}, \ldots u_{d}\right)\) champ de vecteur

  • \(\nabla u=\left(\partial_{x_{j}} u_{i}\right)_{i, j}:\) gradient de \(u(\text { matrice jacobienne })\)

  • \(\varepsilon(u)=\frac{1}{2}\left(\nabla u+\nabla u^{T}\right):\) partie symétrique du gradient de \(u\)

  • \(\Delta u=\left(\Delta u_{1}, \ldots, \Delta u_{d}\right)^{T} \in \mathbb{R}^{d}:\) Laplacien du \(u\)

    Calcul matriciel

  • \(A=\left(A_{i, j}\right) \in \mathbb{R}^{d \times d}\) tenseur (matrice)

  • \(\nabla \cdot A=\left(\nabla \cdot A_{1,:}, \ldots, \nabla \cdot A_{d,:}\right)^{T} \in \mathbb{R}^{d}:\) divergence d’un tenseur

  • \(A: B=\sum_{i, j} A_{i, j} B_{i, j} \in \mathbb{R}:\) produit contracté de deux tenseurs

    Espace fonctionnel

  • \(\left(H^{1}(\Omega)\right)^{d}:\) espace de Sobolev vectoriel

Calcul intégral

Proposition: \(\Omega\) ouvert régulier Lipshitz et

  • Formule de Gauss vectorielle: \( u \in\left(H^{1}(\Omega)\right)^{d}\)

\[\int_{\Omega} \nabla \cdot u=\int_{\partial \Omega} u \cdot n\]

  • Formule d’intégration par partie vectorielle: \(A \in\left(H^{1}(\Omega)\right)^{d \times d}, v \in H^{1}(\Omega)\)

\[-\int_{\Omega}(\nabla \cdot A) \cdot v=\int_{\Omega} A: \nabla v-\int_{\partial \Omega}(A n) \cdot v\]

Calcul intégral (suite)

  • Formule de Green vectorielle \(u \in\left(H^{2}(\Omega)\right)^{d}, v \in\left(H^{1}(\Omega)\right)^{d}\)

\[-\int_{\Omega} v \cdot \Delta u=\int_{\Omega} \nabla u: \nabla v-\int_{\partial \Omega} v \cdot(\nabla u n)\]

Méthode élément fini

1) Formulation variationnelle

\(V=\left\{v \in\left(H^{1}(\Omega)\right)^{d}, u=0 \text { sur } \partial \Omega_{D}\right\}:\) espace vectoriel

Formulation faible : trouver \(u \in V\) tel que \(\quad a(u, v)=\ell(v), \quad \forall v \in V\) avec

\[\begin{array}{l} a(u, v)=\frac{1}{2} \int_{\Omega} \mu\left(\nabla u+\nabla u^{T}\right):\left(\nabla v+\nabla v^{T}\right)+\lambda \int_{\Omega}(\nabla \cdot u)(\nabla \cdot v) \\ \ell(v)=\int_{\partial \Omega_{N}} v \cdot h-\int_{\Omega} f \cdot v \end{array}\]

2) Résolution

Déplacement rigide \(z(x)=\alpha+\beta \times x,\) avec \(\alpha, \beta \in \mathbb{R}^{d}\) \(\rightarrow\) composée d’une translation et d’une rotation

Proposition (Inégalité de Korn)

\(\Omega\) Lipshitz. Supposons que \(V \subset\left(H^{1}(\Omega)\right)^{d},\) s.e.v, ne contient aucun déplacement rigide autre que 0. II existe \(\kappa>0\) tel que

\[\forall v \in V, \quad \kappa\|u\|_{H_{\Omega}^{1}} \leqslant\|\varepsilon(u)\|_{L^{2}}\]

\(\rightarrow a\) est coercive \(\rightarrow a\) est bilinéaire continue sur \(V \times V\) \(\rightarrow \ell\) est linéaire continue sur \(V\) Soit \(\Omega\) Lipshitz, \(f \in\left(L^{2}(\Omega)\right)^{d}\) et \(g \in L^{2}\left(\partial \Omega_{N}\right) .\) Alors le problème a une unique solution dans \(V\).

Discretisation

3) Choix du maillage \(\overrightarrow{\mathcal{T}}_{h}=\left\{K_{i}\right\}\) maillage affine

4) Choix de l’espace \(V_{h}\)

\[P_{h}^{k}=\left\{v_{h} \in C(\bar{\Omega})^{d}, \quad \forall K \in \mathcal{T}_{h}, v_{h | K} \in \mathbb{P}_{k}^{d}, v_{h}=0 \text { sur } \partial \Omega_{D}\right\} \in V\]

5). Construction de la base d’eléments finis: Lagrange

6) Convergence

Proposition

\(\Omega\) polyédrique et \(\left(\mathcal{T}_{h}\right)\) une famille régulière de triangulations.

Soit \(f \in L^{2}(\Omega)\) et \(u \in V\) la solution du problème.

Soit \(u_{h} \in P_{h}^{k}\) la solution approché du problème d’élasticité linéaire. Alors

\[\left\|u-u_{h}\right\|_{\left(H^{1}(\Omega)\right)^{d}} \rightarrow 0\]

6) Convergence

Si de plus \(u \in\left(H^{k+1}(\Omega)\right)^{d} \cap V,\) alors

\[\left\|u-u_{h}\right\|_{\left(H^{1}(\Omega)\right)^{d}} \leqslant C h^{k}\|u\|_{L^{2}}\]

  • \(\rightarrow\) Pour les éléments fini d’ordre \(P^{k},\) la convergence est d’ordre \(O\left(h^{k}\right)\) à la condition que la solution exacte soit suffisamment régulière.

  • \(\rightarrow\) Pas de convergence dans \(L^{2}\) d’ordre \(O\left(h^{k+1}\right)\) car pas d’équivalent de Lemme d’Aubin Nitsche pour ce problème.

Perte de coercivité

Propriété de \(a\) bilinéaire :

\[\begin{array}{ll} \|a(u, v)\| & \leqslant M(\lambda+\mu)\|u\|\|v\| & \text { (continuité) } \\ \|a(u, u)\| & \geqslant \kappa \mu\|v\|^{2} & \text { (coercivité) } \end{array}\]

Preuve de la convergence pour \(u \in\left(H^{k+1}(\Omega)\right)^{d} \cap V:\)

\[\begin{aligned} \left\|u-u_{h}\right\| \leqslant \frac{M}{\kappa} \frac{(\lambda+\mu)}{\mu} \operatorname{dist}\left(u, V_{h}\right) & \leqslant \frac{M}{\kappa} \frac{(\lambda+\mu)}{\mu}\left\|u-\mathcal{I}_{V_{h}}(u)\right\| \leqslant \frac{M}{\kappa} \frac{(\lambda+\mu)}{\mu} C h^{k}\|u\|_{H^{k+1}} \end{aligned}\]

  • \(\rightarrow\) quand \(\lambda / \mu\) est très grand, mauvais contrôle de l’erreur

  • \(\rightarrow\) Coeff. de Poisson \(\nu=\frac{1}{2} \frac{\lambda}{\lambda+\mu}\left(\leqslant \frac{1}{2}\right)\) tend vers \(1 / 2\) quand \(\lambda / \mu \rightarrow+\infty\), on a \(\lambda=\frac{E \nu}{(1+\nu)(1-2\nu)},\, \mu = \frac{E}{2(1+\nu)}\)

  • \(\rightarrow\) limite d’incompressibilité

Feel++

References

Manuel

http://docs.feelpp.org/toolboxes/0.108/

Examples and Benchmarks

http://docs.feelpp.org/cases/0.108/

Feel++ pipeline

Failed to generate image: Could not find the 'blockdiag', 'blockdiag3' executable in PATH; add it to the PATH or specify its location using the 'blockdiag' document attribute
blockdiag {
   // Set labels to nodes.
   A [label = "geometry or mesh .geo, .json/h5"];
   B [label = "modeling .json"];
   C [label = "configuration .cfg"];
   D [label = "feelpp toolbox"];
   E [label = "logs"];
   F [label = "paraview files: .case"];
   // Set labels to edges. (short text only)
   B -> D [label = "config"];
   A -> D [label = "mesh generation"];
   C -> D [label = "config"];
   D -> F [label = "generate"];
   D -> E [label = "produce"];
}

Docker

> docker pull feelpp/feelpp-toolboxes
> docker run --rm -it -v $HOME/csmi:/feel feelpp/feelpp-toolboxes
the docker image is bigger than feelpp/feelpp. feelpp/feelpp is contained in feelpp/feelpp-toolboxes. You may want to remove feelpp/feelpp to preserve space.
# remove image
> docker rmi feelpp/feelpp
# cleanup system from dangling images
> docker system prune

Exemples