TP Mécanique des Solides et Mécanique des Fluides

Tip	l’énoncé est ici.

Elasticité Linéaire

Le TP est à effectuer avec la toolbox feelpp_toolbox_solid.

Partie 1

On considère le domaine suivant soit $\Omega=]0, L[\times ] 0,1[ $ et l’on note $\Gamma_{i}$ les quatre côtés du bord, numérotés dans le sens inverse des aiguilles d’une montre et avec $\Gamma_{1}$ le bord du bas.

Le problème d’élasticité linéaire s’écrit:

\[\begin{aligned} \nabla \cdot \sigma(u) &=f \mbox{ dans } \Omega\\ \sigma(u) &=2 \mu \varepsilon(u) + \lambda(\nabla \cdot u) \mathrm{Id}\\ u&=0 \mbox{ sur } \Gamma_{1} \\ \sigma(u) n& =0 \mbox{ sur } \Gamma_{2} \cup \Gamma_{3} \cup \Gamma_{3} \end{aligned}\]

avec $\lambda, \mu$ les coefficients de Lamé

Créer le maillage du domaine $\Omega$.
Ecrire la formulation variationnelle, puis mettre en place la configuration pour Feel++ en prenant pour données $f=(0,1)^{T}$ et $\mu=\lambda=1$
Visualiser la déformation du maillage obtenue à l’aide la fonction WarpByVector

Ajouter sur le maillage déformé la visualisation de la norme de Frobénius du tenseur des contrainte $\sigma(u)$ ainsi que des champs Von-Mises et Tresca. Commenter en vous aidant d’une petite recherche sur les champs précédents (Von-Mises…) par exemple sur Wikipedia.

Partie 2: Perte de coercivité.

On ajoute à présent deux trous circulaires dans le domaine précédent.

Figure 1. Poutre trouée

On fixe la poutre sur les bords gauche et droite et on la pince: on exerce donc une pression constante sur le bord du bas (force dirigée vers le haut) et sur le bord du haut (force dirigée vers le bas).

Créer le maillage et la configuration Feel++ associé au problème.
Comparer les solutions obtenues avec $\lambda / \mu=1$ et $\lambda / \mu=10^{3} .$ Afficher les lignes de niveau associé au déplacement vectical $u_{2} .$ À cette fin, on utilisera le préconditionneur diagonal (Jacobi) --solid.pc-type jacobi et on affichera les itérations --solid.ksp-monitor=1. Commenter.

Stokes

Partie 1: Eléments finis stables.

On considère le problème de Stokes suivant:

\[\begin{aligned} -\Delta u+\nabla p &=f \text{ dans } \Omega \times \mathbb{R}^{+} \\ \nabla \cdot u &=0 \\ u&=g \text{ sur } \partial \Omega \times \mathbb{R}^{+} \end{aligned}\]

Une solution exacte est donnée par la solution de Kovasznay:

\[u=\left[\begin{array}{c} 1-e^{\lambda x} \cos (2 \pi y) \\ \frac{\lambda}{2 \pi} e^{\lambda x} \sin (2 \pi y) \end{array}\right], \quad p(x, y)=-\frac{e^{2 \lambda x}}{2}+C\]

avec $\lambda=1 /(2 \nu)-\sqrt{1 /\left(4 \nu^{2}\right)+4 \pi^{2}}, C \in \mathbb{R}$ une constante et le second membre $f$ est déterminé de telle sorte que $u$ soit solution.

On considère le domaine $\Omega=(-0.5,1) \times(-0.5,1.5)$ et $\nu=0.035 .$ Les conditions de Dirichlet sur le bord sont obtenues en évaluant la solution exacte.

Déterminer $f$ de telle sorte que $u$ soit solution puis $C \in \mathbb{R}$ tel que $p$ soit à moyenne nulle sur $\Omega$.
Créer le maillage du domaine $\Omega$.
Ecrire la formulation variationnelle pour le problème suivant:

\begin{aligned} -\Delta u+\nabla p&=f, \quad \text{dans} \Omega\\ \nabla \cdot u &=0 \\ u &=g \text{ sur } \partial \Omega \end{aligned}

Considérer les éléments $P_{2} / P_{1}$ et calculer la moyenne de la pression. Commenter.
Faire une analyse de convergence en vitesse et pression pour les éléments $P_{2} / P_{1}$.

Partie 2: Navier-Stokes instationnaire.

On considère le problème suivant

\[\begin{aligned} \partial_{t} u + ( u \cdot \nabla ) u -\nu \Delta u+\nabla p &=f, & & \text { dans } \Omega \times[0, T] \\ \nabla \cdot u &=0 & & \\ u &=g_{D}, & & \operatorname{sur} \Gamma_{i n} \times[0, T] \\ u &=0, & & \operatorname{sur} \Gamma_{0} \times[0, T] \\ \nu \partial_{n} u-p n &=g_{N}, & & \operatorname{sur} \Gamma_{o u t} \times[0, T] \\ u(0, x) &=u_{i n i t}(x), & & \operatorname{sur} \Gamma \end{aligned}\]

où

$u: \Omega \times[0, T] \rightarrow \mathbb{R}^{2}$ est le champ de vitesse,
$p: \Omega \times[0, T] \rightarrow \mathbb{R}$ la pression.

Le bord du domaine est décomposée en 3 partie $: \partial \Omega=\Gamma_{i n} \cup \Gamma_{\text {out}} \cup \Gamma_{0}$.

Effectuer une semi-discrétisation en temps et écrire le problème variationnel. On approchera $u^{n+1}\cdot \nabla u^{n+1}$ par $u^{n}\cdot \nabla u^{n+1}$.

On considère le domaine suivant

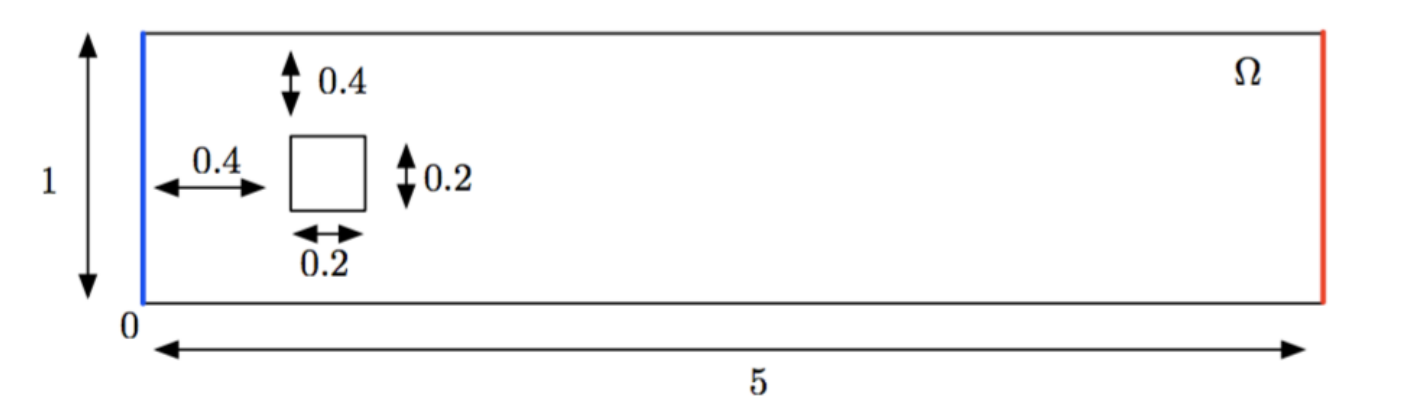
Sur la partie bleue du bord $\left(\Gamma_{i n}\right),$ on impose un profile de vitesse parabolique $ g_{D}(x, y)=(4 y(1-y), 0)^{T}$
Sur les parties noires du bord $\left(\Gamma_{0}\right),$ on impose des conditions de Dirichlet homogène : $g_{D}(x, y)=(0,0)^{T}$
Sur la partie rouge du bord ($\Gamma _{\text {out}}$ ) aucune contrainte n’est exercée (sortie libre): cela correspond à des conditions de type Neumann homogène : $g_{N}(x, y)=(0,0)^{T} .$
Enfin, aucune force extérieure n’est exercée sur le fluide : $f=0$

La donnée initiale est donnée par:

\[u_{i n i t}(x, y)=\left\{\begin{array}{ll} (4 y(1-y), 0)^{T}, & \text { si }(x, y) \in \Gamma_{i n} \\ (0,0)^{T}, & \text { sinon. } \end{array}\right.\]

et les paramètres sont $\nu=0.05$ et $T=10s.$

Programmer la méthode avec la toolbox fluid(CFD) en mode Navier-Stokes
Calculer le trainée et la portance(les composantes de la force qui s’applique sur l’obstacle), les afficher et commenter
Diminuer la viscosité du fluide(prenez quatre valeurs différentes $5e-3, 5e-4, 1e-4, 5e-5$), qu’observez vous ? Commenter en introduisant le nombre de Reynolds $Re=\frac{\rho U L}{\nu}$ avec $\rho=1, U=1, L=0.4$ et en vous documentant sur ce dernier.
Calculer le trainée et la portance(les composantes de la force qui s’applique sur l’obstacle), les afficher et commenter

Tip	la force qui s’applique sur l’obstacle peut être calculée via l’étape de postprocessing de Feel++, voir ici.

Vous utiliserez ce fichier de configuration comme base pour vos différentes simulations

fichier de configuration cfd.cfg

directory=toolboxes/fluid/flow_past_square/cfd3/P2P1G1

[case]
dimension=2

[fluid]
filename=$cfgdir/cfd3.json

mesh.filename=$cfgdir/cfd.geo
gmsh.hsize=0.03
linearsystem-cst-update=false
jacobian-linear-update=false
solver=Oseen #Oseen,Picard,Newton
pc-type=lu #gasm,lu

[fluid.bdf]
order=2
#strategy-high-order-start=1

[ts]
time-step=0.01
time-final=10
#restart=true
restart.at-last-save=true
#time-initial=0.0002
#save.freq=2

la ligne de commande :

mpîrun -np 4 feelpp_toolbox_fluid --config-file cfd.cfg

Execution des codes

Vous pouvez travailler sous vscode avec container ou bien sur atlas.math.unistra.fr.

VSCode/Docker

Concernant VSCode/Docker, afin d’accéder à vos résultats:

lancer un terminal sous vscode. le répertoire dans lequel vous êtes est accessible depuis l’extérieur (et donc eg paraview pour la visu).
taper la commande

export FEELPP_REPOSITORY=$PWD

VSCode Atlas

Concernant la connection à atlas.math.unistra.fr, vous avez eu un compte créé lors du S1 qui est toujours ouvert. Vous vous connectez sur ce compte via VPN.

une fois la connection vpn en place, créer une connection remote-ssh via vscode sur atlas.math.unistra.fr ou bien connectez vous via ssh.

Module Feel++

Pour accéder aux applications Feel++, tapez

module load feelpp-toolboxes/develop_gcc830_openmpi402

Les applications feelpp_toolbox_fluid et feelpp_toolbox_solid sont à présent disponibles.

git est disponible et vous pourrez cloner votre repo du TP sur Atlas.

Visualisation

Nous n’avons pas encore d’outils de visualisation à distance, pour visualiser les résultats il vous faut rapatrier les résultats de calculs sur votre machine et les visualiser avec paraview. Pour cela, utilisez rsync qui ne va rapatrier que les fichiers qui ont été modifiés

Ligne de commande avec rsync pour rapatrier les données

rsync -avz <votre login>atlas.math.unistra.fr:~/feel $HOME/

Cette commande va créer le répertoire $HOME/feel et va télécharger les fichiers depuis la dernière commande rsync.

Pour visualiser le contenu de fichier CSV (les mesures de force par exemple) vous pouvez utiliser excel, google/spreadsheet, python/matplotlib ou paraview. En abcisse le temps en ordonnée la série que vous désirez observer.