Série 5 : Méthodes itératives pour la résolution de systèmes linéaires
1. Théorique
Solution
-
Les valeurs propres de \(P^{-1}A\) son strictement positives,
\[\sigma(P^{-1}A)=\left\{ 1\pm\frac{5}{6},1 \right\}.\]Par la théorie on a
\[\alpha_{opt}=\frac{2}{\lambda_{min}+\lambda_{max}},\]donc \(\alpha_{opt}=1\).
-
Par la théorie on sait que
\[C=\frac{K_2(P^{-1}A)-1}{K_2(P^{-1}A)+1},\]et comme \(P^{-1}A\) est symétrique et définie positive on a \(K_2(P^{-1}A)=\lambda_{max}/ \lambda_{min}\). Alors \(C=5/6\).
-
On a
\[\|\mathbf{x}^{(k)} - \mathbf{x}\|_{A} \leq C \|\mathbf{x}^{(k-1)} - \mathbf{x}\|_{A} \leq C^{k} \|\mathbf{x}^{(0)} - \mathbf{x}\|_{A}.\]D’ailleurs on a aussi
\[\begin{gathered} \|\mathbf{x}^{(0)} - \mathbf{x}\|_{A} \leq \|\mathbf{x}^{(0)} - \mathbf{x}^{(1)}\|_{A} + \|\mathbf{x}^{(1)} - \mathbf{x}\|_{A} \leq \|\mathbf{x}^{(0)} - \mathbf{x}^{(1)}\|_{A} + C \|\mathbf{x}^{(0)}-\mathbf{x}\|_{A} \\ \Longrightarrow \|\mathbf{x}^{(0)} - \mathbf{x}\|_{A} \leq \frac{1}{1-C}\|\mathbf{x}^{(1)} - \mathbf{x}^{(0)}\|_{A} \end{gathered}\]et on a bien le résultat cherché.
-
On utilise la méthode stationnaire pour calculer \(\mathbf{x}^{(1)}\). On a \(\mathbf{x}^{(0)} = (0, 0, 0)^T\) et \(\mathbf{r}^{(0)} = \mathbf{b}\). Donc (avec \(\alpha_{opt}=1\))
\[\begin{aligned} & \mathbf{x}^{(1)} = P^{-1}\mathbf{r}^{(0)} = \left(\frac{1}{6}, \frac{1}{3}, -\frac{1}{2} \right)^{T} \quad \text{et} \\ & \|\mathbf{x}^{(1)} - \mathbf{x}^{(0)}\|_{A} = \|\mathbf{x}^{(1)}\|_{A} =\sqrt{(\mathbf{x}^{(1)}, A \mathbf{x}^{(1)})} = \sqrt{\frac{2}{3}}. \end{aligned}\]On impose donc
\[\|\mathbf{x}^{(k)} - \mathbf{x}\|_{A} \leq 6 \left(\frac{5}{6}\right)^{k} \sqrt{\frac{2}{3}} \leq 10^{-8}\Longrightarrow k \geq \frac{8 + \log_{10} \sqrt{24}}{\log_{10} 6/5} \approx %118.5. 109.7.\]
Solution
D’abord on définit la matrice \(A\) et on vérifie qu’elle est définie positive. La symétrie est évidente.
import numpy as np
import matplotlib.pyplot as plt
n = 5 # ou tout autre nombre approprié
A = 2 * np.diag(np.ones(n)) - np.diag(np.ones(n - 1), -1) - np.diag(np.ones(n - 1), 1)
np.min(np.linalg.eigvals(A))+ Donc la matrice \(A\) est s.d.p. et par conséquence la méthode SOR converge pour \(0<\omega<2\). Les commandes suivantes définissent la partie diagonale, triangulaire inférieure et supérieure de \(A\) ainsi que quelques paramètres pour effectuer la méthode SOR et le membre de droite \(\mathbf{b}\):
D = np.diag(np.diag(A))
E = -np.tril(A, -1)
F = -np.triu(A, 1)
NMAX = 10000
TOL = 1e-9
X0 = np.zeros(n)
b = A @ np.ones(n)+ La boucle "for" suivante calcule pour chaque \(\omega=0, 0.1, \ldots, 2\) le rayon spectral de la matrice d’itération ainsi que la solution de la méthode, et puis sauvegarde le nombre d’itérations nécessaires:
# Note: La fonction sor() doit être définie ou importée
count = 0
omega_range = np.arange(0, 2.1, 0.1)
rho = []
iter = []
for omega in omega_range:
count += 1
B = np.linalg.inv(np.eye(n) - omega * np.linalg.inv(D) @ E) @ ((1 - omega) * np.eye(n) + omega * np.linalg.inv(D) @ F)
rho.append(max(abs(np.linalg.eigvals(B))))
# X, ITER = sor(A, b, X0, NMAX, TOL, omega)
# iter.append(ITER)+ Finalement on affiche le résultat:
plt.figure(1)
plt.plot(omega_range, rho)
plt.figure(2)
plt.plot(omega_range, iter)
plt.show()+ Les graphiques sont illustrés dans la Fig. 1.
Finalement on calcule \(\omega_{opt}\) et le nombre d’itérations correspondant, ainsi que pour \(\omega=1\).
m, argm = min((val, idx) for (idx, val) in enumerate(rho))
omega_opt = omega_range[argm]
iter_at_omega_opt = iter[argm]
arg1 = np.where(omega_range == 1)[0][0]
iter_at_omega_1 = iter[arg1]+ Donc on gagne un facteur 5.3721 en nombre d’itérations par rapport à la méthode de Gauss-Seidel (\(\omega=1\))!
Solution
-
Le minimum de la fonction \(\alpha\in \mathbb{R}\longrightarrow\Phi(\mathbf{x}^{(k)}+\alpha\mathbf{r}^{(k)})\), est atteint dans le point \(\alpha^*\) où la dérivée s’annule, autrement dit,
\[\begin{aligned} 0&=\left.\frac{d}{d\alpha}\Phi(\mathbf{x}^{(k)}+\alpha\mathbf{r}^{(k)})\right|_{\alpha=\alpha^*}\\ &=(\nabla\Phi(\mathbf{x}^{(k)}+\alpha^*\mathbf{r}^{(k)}),\mathbf{r}^{(k)} )\\ &=(A(\mathbf{x}^{(k)}+\alpha^*\mathbf{r}^{(k)})-\mathbf{b},\mathbf{r}^{(k)} )\\ &=(\alpha^*A\mathbf{r}^{(k)}-\mathbf{r}^{(k)},\mathbf{r}^{(k)})\\ &=\alpha^*(A\mathbf{r}^{(k)},\mathbf{r}^{(k)})-(\mathbf{r}^{(k)},\mathbf{r}^{(k)}), \end{aligned}\]ce qui donne \(\alpha^*=\alpha_k\).
-
D’après le point précédent on a
\[0=(\nabla\Phi(\mathbf{x}^{(k)}+\alpha_k\mathbf{r}^{(k)}),\mathbf{r}^{(k)} )= (\nabla\Phi(\mathbf{x}^{(k+1)}),\mathbf{r}^{(k)} )=-(\mathbf{r}^{(k+1)}, \mathbf{r}^{(k)}).\] -
Le problème est de déterminer le minimiseur \({\mathbf{x}}\) de \(\Phi\) en partant d’un point \({\mathbf{x}}^{(0)} \in \mathbb{R}^n\), ce qui revient à déterminer des directions de déplacement qui permettent de se rapprocher le plus possible de la solution x. L’idée la plus naturelle est de prendre la direction de descente de pente maximale \(\mathbf{r}^{(k)}=-\nabla \Phi({\mathbf{x}}^{(k)})\). Puis, chaque itérant \({\mathbf{x}}^{(k)}\) minimise \(\Phi\) le long de cette direction de descente. Ainsi, les directions sont consécutivement orthogonales.
Solution
-
Nous observons que \(A\) est symétrique. On sait que \(A\) est définit positive si et seulement si tout ces sous-matrices principales sont de déterminant positif. On a que \(|A_1|=2>0\) et que \(|A|=|A_2|=3>0\). En conséquence la matrice \(A\) est symétrique et définie positive.
-
Pour \(k=0\), on obtient
\[\alpha_0 = \frac12,\quad \mathbf{x}^{(1)}=\begin{bmatrix} 3/2\\ 5/4 \end{bmatrix}, \quad \mathbf{r}^{(1)}=\begin{bmatrix} -3/4\\ 0 \end{bmatrix}, \quad \beta_0 = -\frac14,\quad \mathbf{p}^{(1)}=\begin{bmatrix} -3/4\\ -3/8 \end{bmatrix}.\]Pour l’itération suivant on obtient
\[\alpha_1 = \frac23,\quad \mathbf{x}^{(2)}=\begin{bmatrix} 1\\ 1 \end{bmatrix}.\]On peut vérifier que \(\mathbf{x}^{(2)}\) est la solution du système.
-
La solution est dessinée dans la figure suivante.
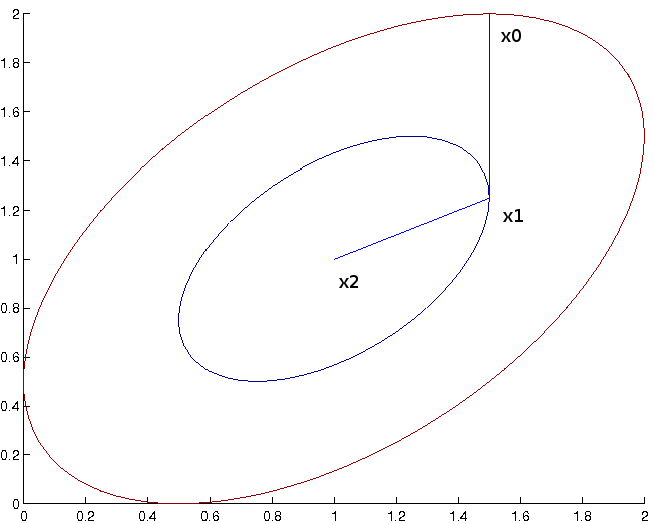
voici le code qui permet de l’obtenir
import numpy as np
# Définir A et b
A = np.array([[2, -1], [-1, 2]])
b = np.array([1, 1])
# Vérifier si A est symétrique définie positive
if np.allclose(A, A.T) and np.all(np.linalg.eigvals(A) > 0):
print("A est symétrique définie positive.")
else:
print("A n'est pas symétrique définie positive.")
# Méthode du gradient conjugué
def conjugate_gradient(A, b, x0, tol=1e-10, max_iter=1000):
x = x0
r = b - np.dot(A, x)
d = r.copy()
rs_old = np.dot(r.T, r)
x_list = [x.copy()]
for i in range(max_iter):
Ad = np.dot(A, d)
alpha = rs_old / np.dot(d.T, Ad)
x += alpha * d
r -= alpha * Ad
rs_new = np.dot(r.T, r)
if np.sqrt(rs_new) < tol:
break
d = r + (rs_new / rs_old) * d
rs_old = rs_new
x_list.append(x.copy())
return x, x_list
# Appliquer la méthode
x0 = np.array([1.5, 2])
x_sol, x_list = conjugate_gradient(A, b, x0, max_iter=2)
print( f"x_list={x_list}, x_sol={x_sol}" )
# Fonctionnelle d'énergie Phi
def phi(x):
return 0.5 * np.dot(x, A @ x) - np.dot(b, x)
# Tracer les lignes de niveau de Phi
x_vals = np.linspace(0, 2, 400)
y_vals = np.linspace(0, 2, 400)
X, Y = np.meshgrid(x_vals, y_vals)
Z = np.array([[phi(np.array([x, y])) for x, y in zip(x_row, y_row)] for x_row, y_row in zip(X, Y)])
phi_levels = sorted([phi(x) for x in x_list])
import plotly.graph_objs as go
# Créer la figure avec les lignes de niveau
fig = go.Figure(data =
go.Contour(
z=Z,
x=x_vals,
y=y_vals,
contours=dict(
start=min(phi_levels),
end=max(phi_levels),
size=int(max(phi_levels)/len(phi_levels))
),
colorscale='Blues'
)
)
# Ajouter les points et les annotations
for i, point in enumerate(x_list):
fig.add_trace(go.Scatter(x=[point[0]], y=[point[1]], mode='markers+text',
text=[f'x^{i}'],
textposition="bottom center",
marker=dict(color='red', size=10)))
# Ajouter x_sol
fig.add_trace(go.Scatter(x=[x_sol[0]], y=[x_sol[1]], mode='markers',
marker=dict(color='green', size=10)))
# Tracer les segments entre les points
for i in range(len(x_list) - 1):
fig.add_trace(go.Scatter(x=[x_list[i][0], x_list[i+1][0]],
y=[x_list[i][1], x_list[i+1][1]],
mode='lines',
line=dict(color='red')))
fig.add_trace(go.Scatter(x=[x_list[-1][0], x_sol[0]],
y=[x_list[-1][1], x_sol[1]],
mode='lines',
line=dict(color='red')))
# Mise en forme finale de la figure
fig.update_layout(title='Lignes de niveau de Phi et points de la méthode du gradient conjugué',
xaxis_title='x1',
yaxis_title='x2')
fig.show()Results
A est symétrique définie positive.
x_list=[array([1.5, 2. ]), array([1.5 , 1.25])], x_sol=[1. 1.]
Solution
-
-
On démontre d’abord l’hypothèse initiale. On a que \(\mathbf{p}^{(0)}=\mathbf{r}^{(0)}\) et \(\mathbf{r}^{(1)}=\mathbf{r}^{(0)}-\alpha_0A\mathbf{p}^{(0)}\) où \(\alpha_0\) est donné par
\[\alpha_0 = \frac{\|\mathbf{r}^{(0)}\|_2^2}{(\mathbf{r}^{(0)},A\mathbf{r}^{(0)})}.\]Donc on conclut que \((\mathbf{p}^{(0)},\mathbf{r}^{(1)}) = (\mathbf{r}^{(0)},\mathbf{r}^{(1)}) =0\). De plus \((\mathbf{p}^{(0)},\mathbf{p}^{(1)})_A= (A\mathbf{p}^{(0)},\mathbf{r}^{(1)}-\beta_0\mathbf{p}^{(0)})\) avec
\[\beta_0 = \frac{(A\mathbf{p}^{(0)},\mathbf{r}^{(1)})}{(A\mathbf{p}^{(0)},\mathbf{p}^{(0)})}\]et donc \((\mathbf{p}^{(0)},\mathbf{p}^{(1)})_A=0\).
-
Noter que
\[(\mathbf{p}^{(j)},\mathbf{r}^{(k+1)} ) = (\mathbf{p}^{(j)},\mathbf{r}^{(k)} ) -\alpha_k (A\mathbf{p}^{(j)},\mathbf{p}^{(k)} )\]et noter que pour \(j=0,\ldots,k-1\) les deux produit scalaires du membre de droite s’annule par l’hypothèse de récurrence. Pour \(j=k\) noter que par le choix de
\[\alpha_k = \frac{(\mathbf{p}^{(k)},\mathbf{r}^{(k)})}{(\mathbf{p}^{(k)},A\mathbf{p}^{(k)})}\]et donc par construction, le terme \((\mathbf{p}^{(k)},\mathbf{r}^{(k+1)} )\) s’annule également. En conséquence
\[ (\mathbf{p}^{(j)},\mathbf{r}^{(k+1)} ) = 0 \quad \mbox{pour}\quad j=0,\ldots, k.\]Deuxièmement noter que
\[\begin{aligned} (\mathbf{r}^{(j)},\mathbf{r}^{(k+1)} ) &=& (\mathbf{p}^{(j)},\mathbf{r}^{(k+1)} ) +\beta_{j-1}(\mathbf{p}^{(j-1)},\mathbf{r}^{(k+1)} ) = 0\quad \mbox{pour}\quad j=1,\ldots, k,\\ (\mathbf{r}^{(0)},\mathbf{r}^{(k+1)} ) &=& (\mathbf{p}^{(0)},\mathbf{r}^{(k+1)} )= 0 \end{aligned}\]par [eq1] et donc
\[ (\mathbf{r}^{(j)},\mathbf{r}^{(k+1)} ) = 0 \quad \mbox{pour}\quad j=0,\ldots, k.\]Troisièment observer que
\[ (\mathbf{p}^{(j)},\mathbf{p}^{(k+1)} )_A = (\mathbf{p}^{(j)},\mathbf{r}^{(k+1)} )_A - \beta_k (\mathbf{p}^{(j)},\mathbf{p}^{(k)} )_A.\]Supposons d’abord que \(j<k\). Donc \((\mathbf{p}^{(j)},\mathbf{p}^{(k)} )_A=0\) par hypothèse de récurrence et
\[(\mathbf{p}^{(j)},\mathbf{p}^{(k+1)} )_A = (\mathbf{p}^{(j)},\mathbf{r}^{(k+1)} )_A = (A\mathbf{p}^{(j)},\mathbf{r}^{(k+1)} ) \quad \mbox{pour}\quad j=0,\ldots, k-1.\]Remarquer que \(A\mathbf{p}^{(j)}= \frac{1}{\alpha_j} (\mathbf{r}^{(j)}-\mathbf{r}^{(j+1)})\), en conséquence \(A\mathbf{p}^{(j)} \in \mbox{span}\{\mathbf{r}^{(0)},\ldots,\mathbf{r}^{(k)}\}\), et donc
\[(\mathbf{p}^{(j)},\mathbf{p}^{(k+1)} )_A = \tfrac{1}{\alpha_j} (\mathbf{r}^{(j)},\mathbf{r}^{(k+1)} ) - \tfrac{1}{\alpha_j} (\mathbf{r}^{(j+1)},\mathbf{r}^{(k+1)} ) \quad \mbox{pour}\quad j=0,\ldots, k-1.\]Par [eq3] on conclut que
\[(\mathbf{p}^{(j)},\mathbf{p}^{(k+1)} )_A = 0 \quad \mbox{pour}\quad j=0,\ldots, k-1.\]Supposons ensuite que \(j=k\). En introduisant dans [eq2] le choix
\[\beta_k = \frac{(\mathbf{p}^{(k)},\mathbf{r}^{(k+1)})_A}{(\mathbf{p}^{(k)},\mathbf{p}^{(k)})_A}\]nous amène directement que \((\mathbf{p}^{(k)},\mathbf{p}^{(k+1)} )_A=0\) par construction et donc
\[(\mathbf{p}^{(j)},\mathbf{p}^{(k+1)} )_A = 0 \quad \mbox{pour}\quad j=0,\ldots, k.\] -
On conclut par récurrence.
-
2. Python
Solution
-
On définit d’abord la matrice
Aet le vecteurb:import numpy as np from scipy.linalg import hilbert A = hilbert(5) b = A @ np.ones(5)La matrice
Aest symétrique définie positive (pour vérifier, l’on peut montrer avec la commandenp.linalg.eigvals(A)que les valeurs propres deAsont strictement positives). On peut donc appliquer les méthodes du gradient et du gradient conjugué.La méthode du gradient n’arrive pas à approcher la solution avec une tolérance de \(10^{-15}\) en \(10^5\) itérations, comme on le voit avec la commande suivante:
from tan.syslin import gradient P = np.eye(5) x, iter = gradient(A, b, P, x0=np.zeros(5), tol=1e-15, maxiter=1e5) # gradient reached the maximum iteration number without converging. # # x = # 1.0000 # 1.0004 # 0.9984 # 1.0024 # 0.9988 # iter = # 100000pour utiliser la méthode du gradient non-préconditionné on a choisi le préconditionneur égal à la matrice identité (\(P=I\)). -
De la même façon, on voit que la méthode du gradient préconditionné avec
np.tril(A)converge avec \(92517 < 10^5\) itérations:P = np.tril(A) x, iter = gradient(A, b, P=P, x0=np.zeros(5), tol=1e-15, maxiter= 1e5) # gradient converged in 92517 iterations. # # x = # 1.0000 # 1.0000 # 1.0000 # 1.0000 # 1.0000 # iter = # 92517La proprieté de convergence de la méthode du gradient préconditionné (Richardson dynamique) que l’on a vu au cours a été énoncée dans le cas où \(P\) est symétrique définie positive: ce qui n’est pas le cas avec \(P=\) np.tril(A). Néanmoins, on observe une réduction d’itérations nécessaires pour satisfaire le critère de convergence en dessous de 100'000 itérations. -
On utilise maintenant la méthode du gradient conjugué:
from scipy.sparse.linalg import cg x, info = cg(A, b, tol=1e-15, maxiter=10000) # pcg converged at iteration 8 to a solution with relative residual 2.3e-16 # # x = # 1.0000 # 1.0000 # 1.0000 # 1.0000 # 1.0000Cette méthode converge en seulement \(8\) itérations. Il faut remarquer qu’en précision infinie, la méthode du gradient conjugué converge en au plus \(n\) itérations, où \(n\) est la taille de la matrice du système. Dans cet exercice, \(8>n=5\), à cause des erreurs d’arrondi.
 .pdf
.pdf
 .ipynb
.ipynb