2-Spheres swimmer
The goal of this example is to verify the scallop theorem (Scallop Theorem) by the two sphere swimmer using the feelp fluid toobox.
1. The swimmer model
The two-sphere swimmer is a three dimensional swimmer composed of two spheres of radius \(R\) that are linked by a rigid arm of length \(D\). There is an internal engine on the left sphere that is responsible for changing the length of the arm.
There is only one periodic strategy of motion for the swimmer described in the figure below :
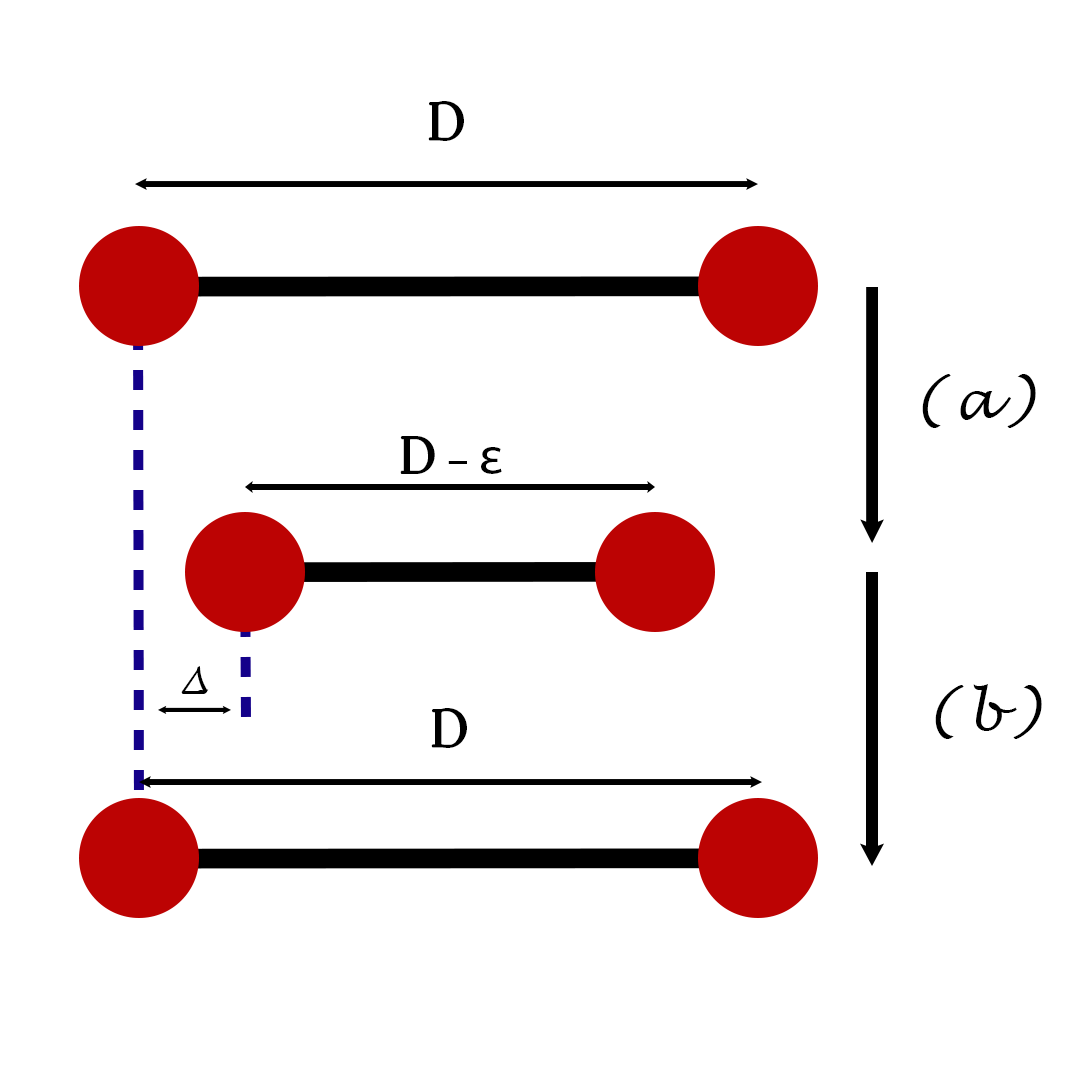
\[\textit{Fig} \;1.\;\; \text{The complete cycle of the motion of the swimmer.}\]
The periodic motion is composed of two strokes :
-
(a) : Retracting the arm then staying fixed for 1s.
-
(b) : elongating the arms then staying fixed for 1s.
The time between two succussive strokes is 1 second, which means, the swimmer performs a stroke and wait one second before performing the next one.
This cyclic motion is obviously reciprocal.
2. The governing equation
The coupled problem describing the motion of the swimmer in a Stokes fluid is given by :
\[ \begin{cases} -\mu\Delta u + \nabla p = f,\qquad\qquad\qquad\qquad \text{in}\;\mathcal{F}_t,\\ \nabla \cdot u = 0,\qquad\qquad\qquad\qquad\qquad\;\;\;\;\; \text{in}\;\mathcal{F}_t,\\ u = \mathbf{U}_i+\mathit{\omega}_i \times(x-x_i^{CM}(t))\qquad\;\;\;\;\;\;\text{on}\;\partial B_i,\\ m_i\dot{\mathbf{U}}_i = -F_{fluid},\qquad\qquad\qquad\qquad\;\; i = 1,2,\\ J_i\dot{\mathit{\omega}}_i = -M_{fluid},\qquad\qquad\qquad\qquad\;\;\; i = 1,2, \end{cases} \]
where :
-
\(u\) : the fluid velocity
-
\(p\) : the fluid pressure
-
\(\mathbf{U}\) : translational speed
-
\(\omega\) : angular speed
-
\(x^{CM}\) : the swimmer’s center of mass
-
\(m\) and \(J\) are the swimmer’s volume and geometric inertia tensors.
-
\(B_1\) and \(B_2\) are the bodies of the left and the right spheres respectivly
-
\(\mathcal{F}_t= \mathbb{R}^3 \backslash\bigcup_{i=1}^{2} B_i\) : the domain occupied by the fluid.
3. geometry
The domain consists of the swimmer described above, put inside a 3D cuboid of dimensions \(L\times l\times l\). The geometry with a 2D meshing is as follow :
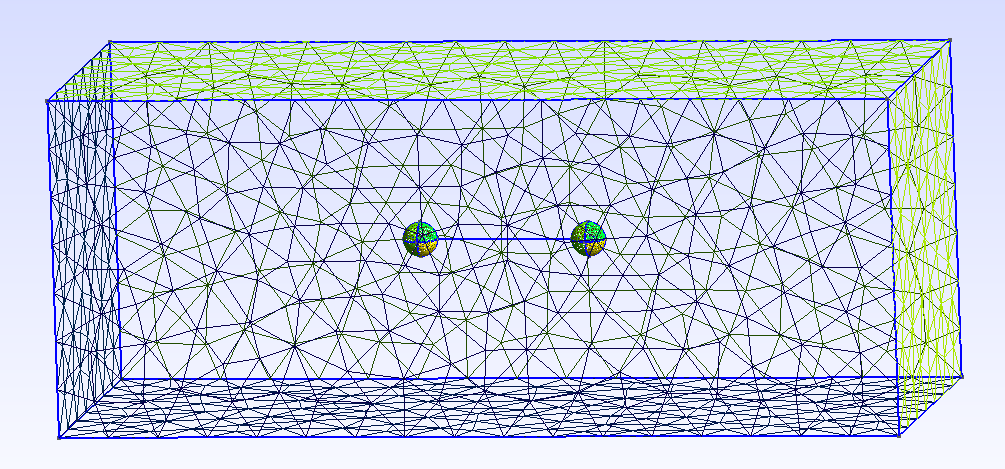
\[\textit{Fig} \;2.\;\; \text{The geometry of the swimmer and the fluid domain.}\]
4. Parameters
Name |
Description |
values |
Unit |
\(R\) |
spheres raduis |
1 |
\(\mu m\) |
\(D\) |
arm length |
\(10R\) |
\(\mu m\) |
\(\varepsilon\) |
relative displacement of the sphere |
\(4R\) |
\(\mu m\) |
\(L\times l\times l\) |
cuboid dimensions |
\(50\times 20\times 20\) |
\(\mu m\times\mu m\times\mu m\) |
5. Materials
Name |
Description |
values |
Unit |
\(\rho_{fluid}\) |
fluid density |
1 |
\(kg/m^3\) |
\(\rho_{spheres}\) |
spheres density |
0.1 |
\(kg/m^3\) |
\(\mu\) |
viscosity |
1 |
\(N.s/m^2\) |
6. Run simulations
The command line to run the simulations is
mpirun -np 4 feelpp_toolbox_fluid --config-file two_sphere.cfg7. Results
7.1. Analytical results
The scallope theorem says that swimmers that perform reciprocal (time reversal) motion can not achieve a net displacement after one period. Since our swimmer has only one degree of freedom and thus has only one strategy of swimming which is reciprocal (described above), then there will be no gained displacement after each period.
7.2. Numerical results
Now, we will check if the numerical results are convinient with the analytical ones.
Using the fluid toolbox to simulate this model, we obtain the figure below :
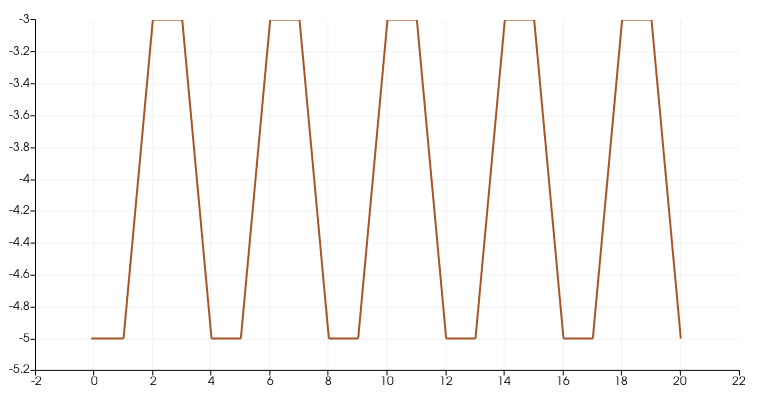
\[\textit{Fig} \;3.\;\; \text{The position of the left sphere during the 2-step strokes.}\]
From this figure, we can see that the displacement gained in the first half of each period is canceled out by the second half of the period. Then, the results obtained are convinient with the scallop theorem.
References on Swimming
-
[Najafi_2004] Ali Najafi, Ramin Golestanian. Simple swimmer at low Reynolds number: Three linked spheres. 2004. American Physical Society. doi.org/10.1103/PhysRevE.69.062901 linkDownload PDF
-
[nature] Jikeli, J., Alvarez, L., Friedrich, B. et al. Sperm navigation along helical paths in 3D chemoattractant landscapes. Nat Commun 6, 7985 (2015). doi.org/10.1038/ncomms8985 Download PDF
-
[bgp_cemracs_2019] Luca Berti, Laetitia Giraldi, Christophe Prud’Homme. Swimming at Low Reynolds Number. ESAIM: Proceedings and Surveys, EDP Sciences, 2019, pp.1 - 10, doi.org/10.1051/proc/202067004 Download PDF
-
[bcgp_three_spheres_2020] Luca Berti, Vincent Chabannes, Laetitia Giraldi, Christophe Prud’Homme. Modeling and finite element simulation of multi-sphere swimmers. 2020. hal-mines-paristech.archives-ouvertes.fr/ENSMP_CEMEF/hal-03023318v1 Download PDF
-
[gbcc_epje_2017] K. Gustavsson, L. Biferale, A. Celani, S. Colabrese Finding Efficient Swimming Strategies in a Three Dimensional Chaotic Flow by Reinforcement Learning Published on Eur. Phys. J. E (December 14, 2017) 10.1140/epje/i2017-11602-9 Download PDF
-
[purcell_1977] E.M. Purcell. Life at Low Reynolds Number, American Journal of Physics vol 45, p. 3-11 (1977). doi.org/10.1119/1.10903 Download PDF
 .pdf
.pdf