Reinforcement learning for the PMPY swimmer
In this example, we study the PMPY swimmer with a reinforcement learning approach coupled with Feel++ fluid toolbox to simulate the interactions between the swimmer and the fluid.
Some swimmers have been studied using this approach :
1. Introduction
Our goal is to apply reinforcement learning to make the PMPY swimmer self-learn its optimal swimming strategy. Here, instead of computing the displacement of the swimmer using theoretical solutions, we couple the reinforcement learning algorithm with Feel++ as we did for the three-sphere swimmer studied in here.
The PMPY swimmer performing a non-reciprocal motion was simulated in 2D and 3D here. The simulations show that the two models have the same behavior although their speeds are not equal. Hence, reinforcement learning will be applied to the 2D model as it requires less time in simulations.
2. Model
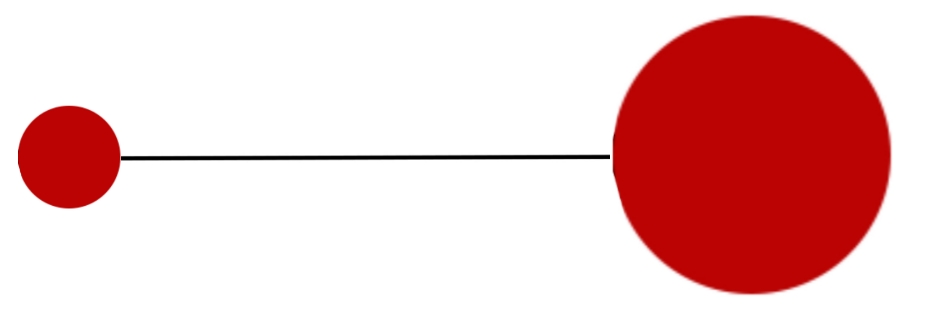
We consider the PMPY swimmer shown in the figure below. The swimmer can exchange the volumes of its spheres and change the length of its arm. Unlike the four-cyclic motion simulated in pmpu, we suppose that the swimmer can change the length of its arm to different lengths and can also exchange volumes of its spheres in different ways.
3. Reinforcement learning
3.1. Q-learning & double Q-learning algorithms
We use the \(Q\)-\(learning\) and \(Double\) \(Q\)-\(learning\) algorithms to self-learn the PMPY how to swim. The \(\varepsilon\)-greedy scheme will be used in reinforcement learning algorithms for a better exploration of the medium.
The algorithms and the \(\varepsilon\)-greedy were presented in details for the three-sphere swimmer here.
3.2. States, actions and reward
As the total volume of the spheres should be conserved, the swimmer can not freely change the volumes of its spheres. For this reason, the swimmer will change (for e.g.) the length of the left sphere while the volume of the right sphere will be changing according to the left one to guarantee the conservation of the total volume. Hence, the actions taken by the swimmer can be described by the change of :
-
length of the arm
-
volume of the left sphere
Let \(v_T\) be the total volume of the spheres. We denote by \(\mathcal{V}_l\) the finite set of possible volumes that the left sphere can take.
\[\mathcal{V}_l = \bigg\{ v_1, v_2, \dots , v_k \big/ k\geq 2\; \text{and}\; 0 <v_i\neq v_{i+1}< v_T\ \bigg\}. \]
Let \(\mathcal{R}_l\) be the set of all the radii that correspond to the volumes of the left sphere given in \(\mathcal{V}_l\). It can be expressed as
\[\mathcal{R}_l = \bigg\{ r_1, r_2, \dots , r_k \big/ r_i = \sqrt{\frac{v_i}{\pi}}\; \text{such that}\; v_i\in\mathcal{V}_l \bigg\}. \]
Let \(L\) be the finite set of the possible length that the arm of the swimmer can take given as follow
\[\mathcal{L} = \bigg\{ \ell_1, \ell_2, \dots , \ell_k \big/ k\geq 2\; \text{and}\;\ell_i\neq\ell_{i+1} \bigg\}. \]
Following these notations, the configurations of the swimmer can be expressed using the radius of the left sphere and the length of its arm. Hence, for \(\mathcal{R}_l\) and \(\mathcal{L}\) given, the space of states can be expressed as follow
\[\mathcal{S}= \mathcal{R}_l\times\mathcal{L}=\bigg\{ (r, \ell) \big/ r\in\mathcal{R}_l\; \text{and}\; \ell\in \mathcal{L} \bigg\}.\]
To move from a state to another, the swimmer changes the length of its arm (to a length given in \(\mathcal{L}\)) or changes the volume of its left sphere to another volume in \(\mathcal{V}_l\). Note that, in our reinforcement learning approach, the swimmer can not change the volume and length of its arm at the same time.
Taking an action in a certain state makes the swimmer move to another position with new configuration. This net displacement will be the rewward that measures the success of taking this action.
The displacement of the swimmer will be computed as follow
\[r = \frac{dx_1+dx_2}{2}, \]
where \(x_1\) and \(x_2\) denote the center of mass of the left and the right spheres respectively.
We note that the swimmer aims to maximize the cumulative reward during the learning process.
3.3. Interaction with the surrounding medium
In our reinforcement learning implementation, the hydrodynamics interations between the swimmer and the surrounding fluid are simulated with the Feel++ fluid toolbox. At each iteration, a simulation of the swimmer performing the the given action (in a specific state) will be ran automatically and the reward will be recovered from a \(csv\) exported by the toolbox.
Since our model is described with Stokes equations, a pair of action-state always gives the same reward (displacement). Hence, each pair of action-state will be simulated once and the reward will be stored (in a matrix for e.g.) to be used without running the same simulation.
4. Data files
Here are the files we used to launch the reinforcement learning process.
-
simulation files generator: this file automatically generates the cfg, geo and json files for simulations.
-
Run simulations: this file is used to run simulations using the generated files.
-
RL functions for PMPY: In this file, we have built functions to adapt reinforcement learning to our model.
-
Launch RL: this file launches the Q-learning and double Q-learning algorithms for our model.
5. Inpute parameters
For our model, we fixe the total volume :
Parameter |
Description |
values |
\(v_T\) |
Total volume of the spheres |
\(5\pi\) |
For the Q-learning algorithm, we set the following parameters :
Parameter |
Description |
values |
\(\alpha\) |
Learning rate |
1 |
\(\gamma\) |
Discount factor |
0.9 |
\(\epsilon\) |
\(\epsilon\)-greedy parameter |
0.1 |
6. Results
6.1. Exemple 1
We start with a simple example in which the swimmer’s arm can have only two possible lengths and the volume of its left sphere can take only two values. We put \(\mathcal{R}_l = \{1, 2\}\) and \(\mathcal{L} = \{6, 10\}\).
In this case, the swimmer has only four different configurations illustrated as follow
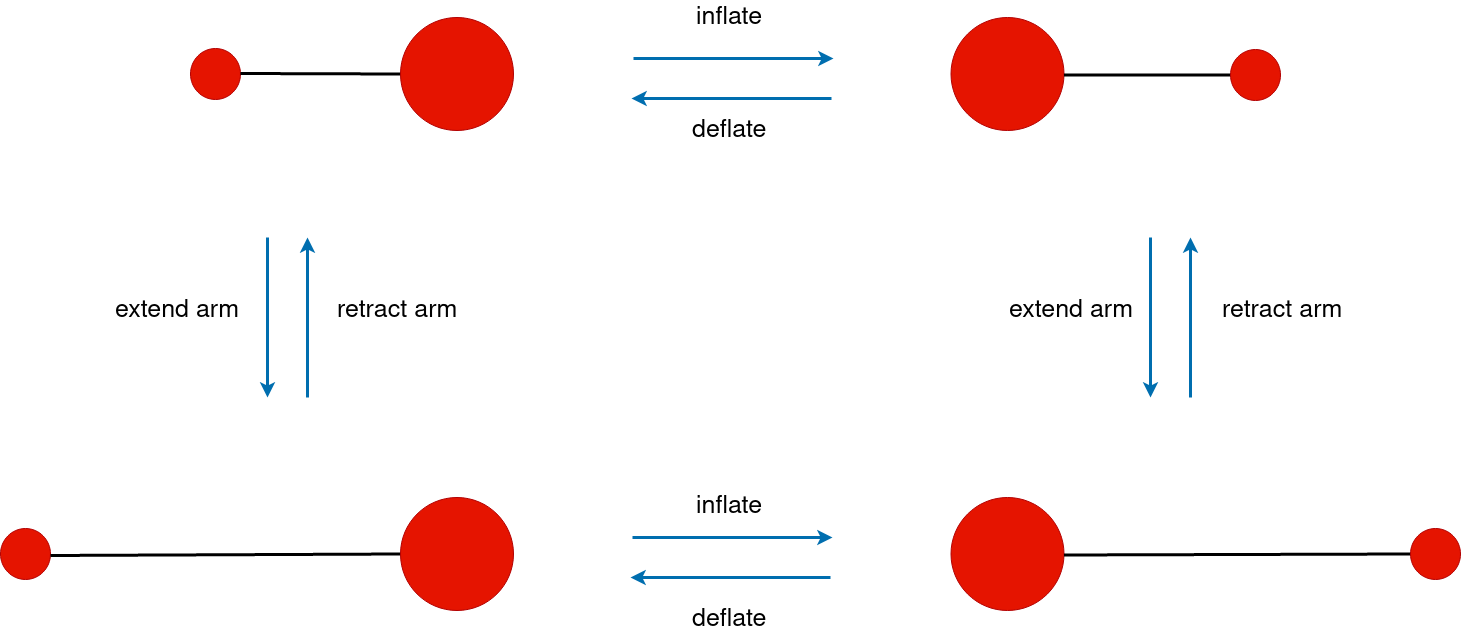
Note that in this case, the swimmer has only one non-reciprocal motion. Hence, there is only one swimming strategy giving a net displacement (the strategy simulated here).
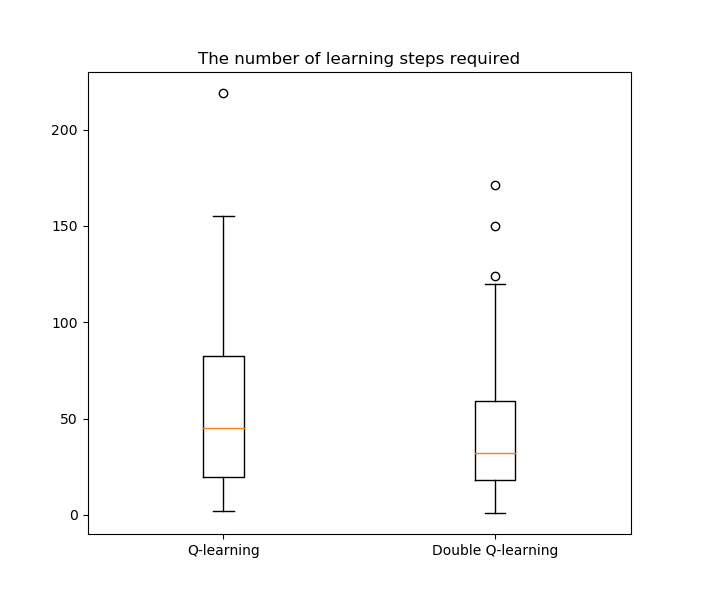
The two figures below show a typical learning process of the PMPY swimmer using Q-learning and double Q-learning algorithms.here
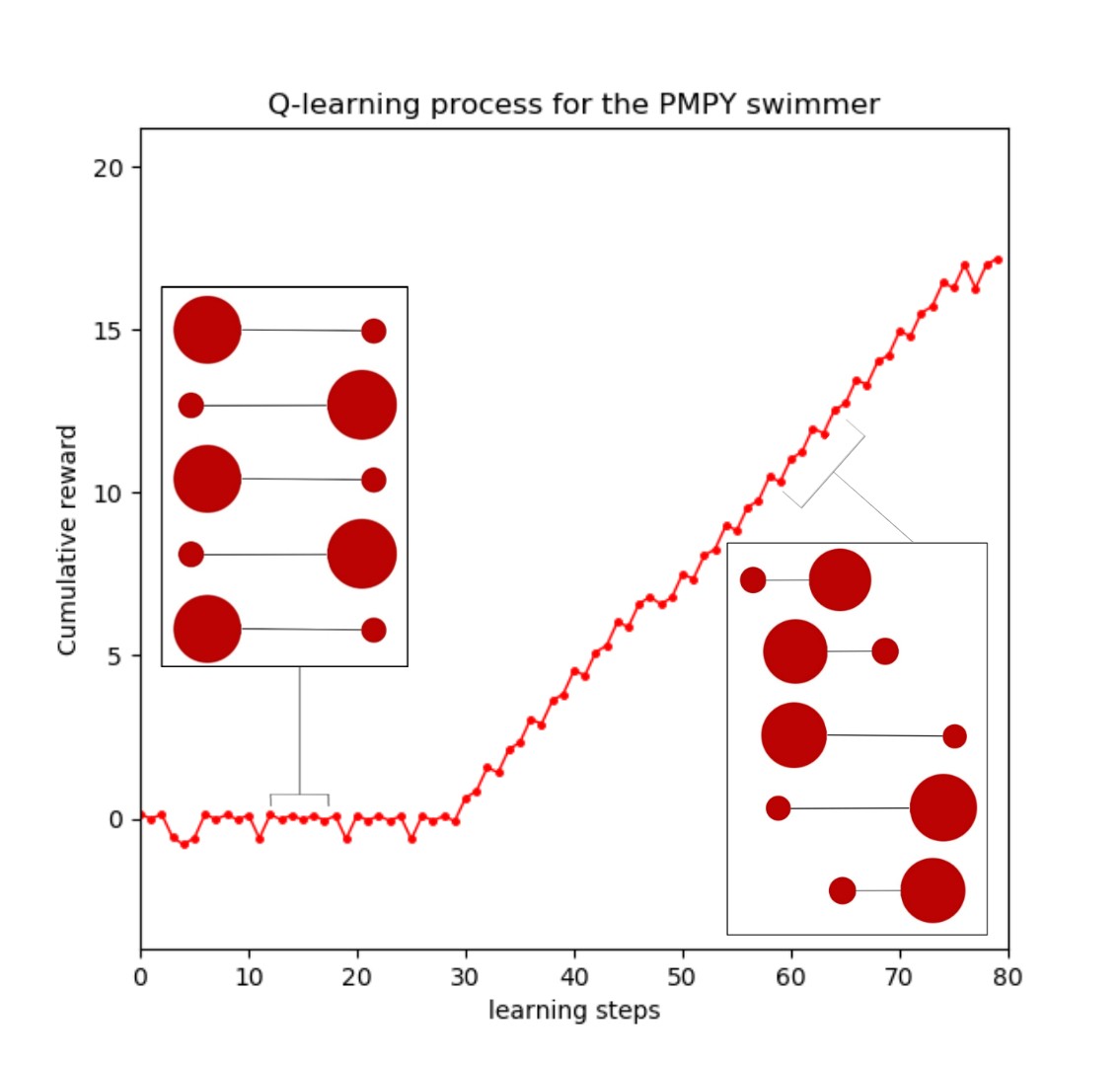
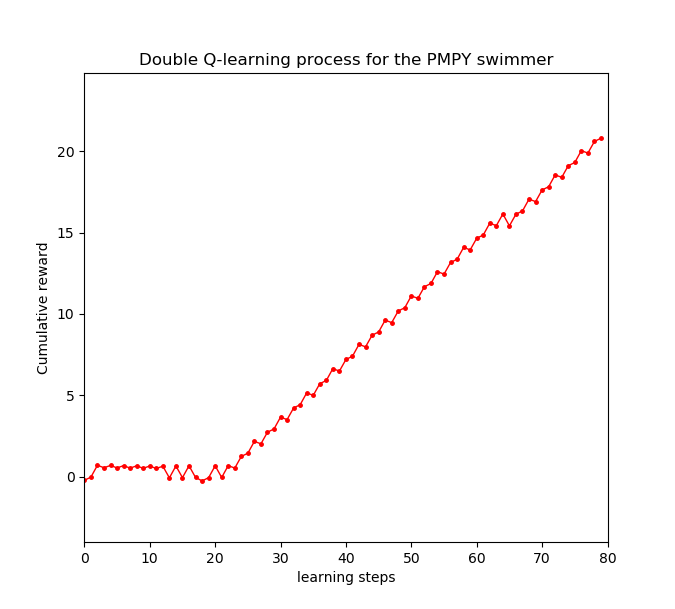
As can be seen, the swimmer has managed to swim by interacting with the surrounding medium. After accumulating enough knowledge (3O learning steps for QL and 20 for double QL), the swimmer finds the non-reciprocal motion that enables it to swim forward.
To investigate the number of learning steps required to learn this pattern. We performed 100 simulations for both Q-learning and double Q-learning algorithms using the same learning parameters mentioned above.
6.2. Exemple 2
In this example, we put \(\mathcal{R}_l = \{1, 1.5, 2\}\) and \(\mathcal{L} = \{6, 8, 10\}\). In this case, the swimmer can perform many non-reciprocal motions. We will show that the swimmer can find the optimal swimming strategy that gives the largest net displacement.
Here, the swimmer has nine different configurations and can perform eight different actions. The optimal swimming strategy.
Note that from the net displacement computed in [Avron_pmpu], it is clear that the optimal gait in our case is the closed path in the \(v-\ell\) plane using the extreme values in \(\mathcal{V}_l\) and \(\mathcal{L}\).
*
*
*
*
References on PMPY swimmer
-
[Avron_pmpu] JE Avron, O Kenneth, and DH Oaknin. _Pushmepullyou: an efficient micro-swimmer. _2005. New Journal of Physics 7.1, p. 234. Download PDF
-
[Silverberg_pmpu] O Silverberg, E Demir, G Mishler, B Hosoume, N Trivedi, C Tisch, D Plascencia, O S Pak & I E Araci. Realization of a push-me-pull-you swimmer at low Reynolds numbers. _2020. Bioinspiration & Biomimetics, 15(6), 064001. Download PDF
References on Learning Methods
-
[gbcc_epje_2017] K. Gustavsson, L. Biferale, A. Celani, S. Colabrese Finding Efficient Swimming Strategies in a Three Dimensional Chaotic Flow by Reinforcement Learning Published on Eur. Phys. J. E (December 14, 2017) 10.1140/epje/i2017-11602-9 Download PDF
-
[Q-learning] Tsang, A.C., Tong, P., Nallan, S., Pak, O.S. (2018). Self-learning how to swim at low Reynolds number. arXiv: Fluid Dynamics.Download PDF
 .pdf
.pdf