Three Sphere Swimmer & Low Reynolds Number \(Re\)

Here, using the Navier-Stokes equation, we check the dependence of the net-displacement of the three-sphere swimmer with the Reynolds number \(Re\).

We use the Navier-Stokes equation with low Reynolds number given by : \[ Re = \frac{\rho UL}{\mu},\] where :

In our example, the viscosity and the density of the fluid are fixed, so the Reynolds number depends on the swimmer’s length and velocity. As we aim to perform many simulations for different values of \(Re\), we change the arm’s length of the swimmer \(D\), and for each simulation, we fix the relative velocity of the swimmer to be \(U = 4R\), where \(R\) is the spheres radius (Note that \(D=10R\)).

We study the 2D-three sphere swimmer studied before with the Stokes equation in 3SS with Navier-Stokes. Note that it was also studied using the Stokes equation in 3-spheres-2D.

We remind that the swimmer consists of three spheres of radius \(R\) linked by two rigid arms of length \(D\).

The swimmer mensionned above is placed at the center of a rectangular channel of dimensions \([-L, L]\times[-l, l]\). See 3-spheres-2D.

The simulations performed for different values of \(D\) in \([5.10^{-7}, 10^{-1}]\). For each simulation, here are the parameters we used (that obviously depend on \(D\)):

For the simulations we performed, we show in the figures below, the relation between the Reynolds number \(Re\) and the dimensionless net-displacement of the swimmer.

The first figure shows the dimensionless net-displacement \(\frac{\Delta}{R}\) in function of the Reynolds number \(Re\) that depends on \(D\) for each simulation.

The second figure presents the same graph with a logarithmic scale in the \(x\)-axis for a better visualization of low values in \(10^{-3}, 10^2\).

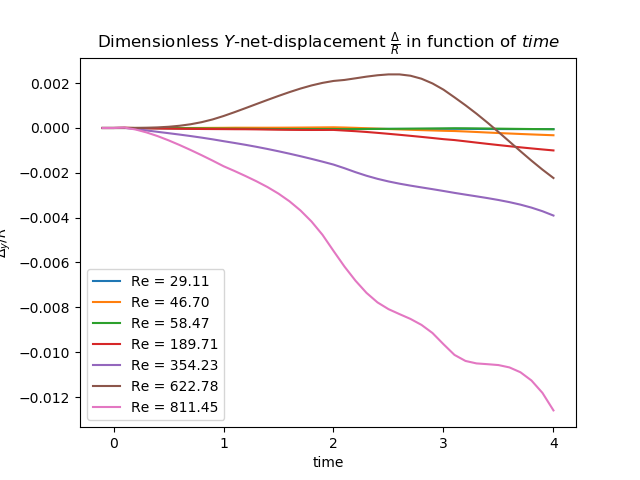
Now we check the \(Y\)-net displacement of the swimmer for different low Reynolds number. The figure below presents the dimensionless \(Y\)-net displacement after one period for some values of \(Re\) mentioned in the figure.