Ray Tracing

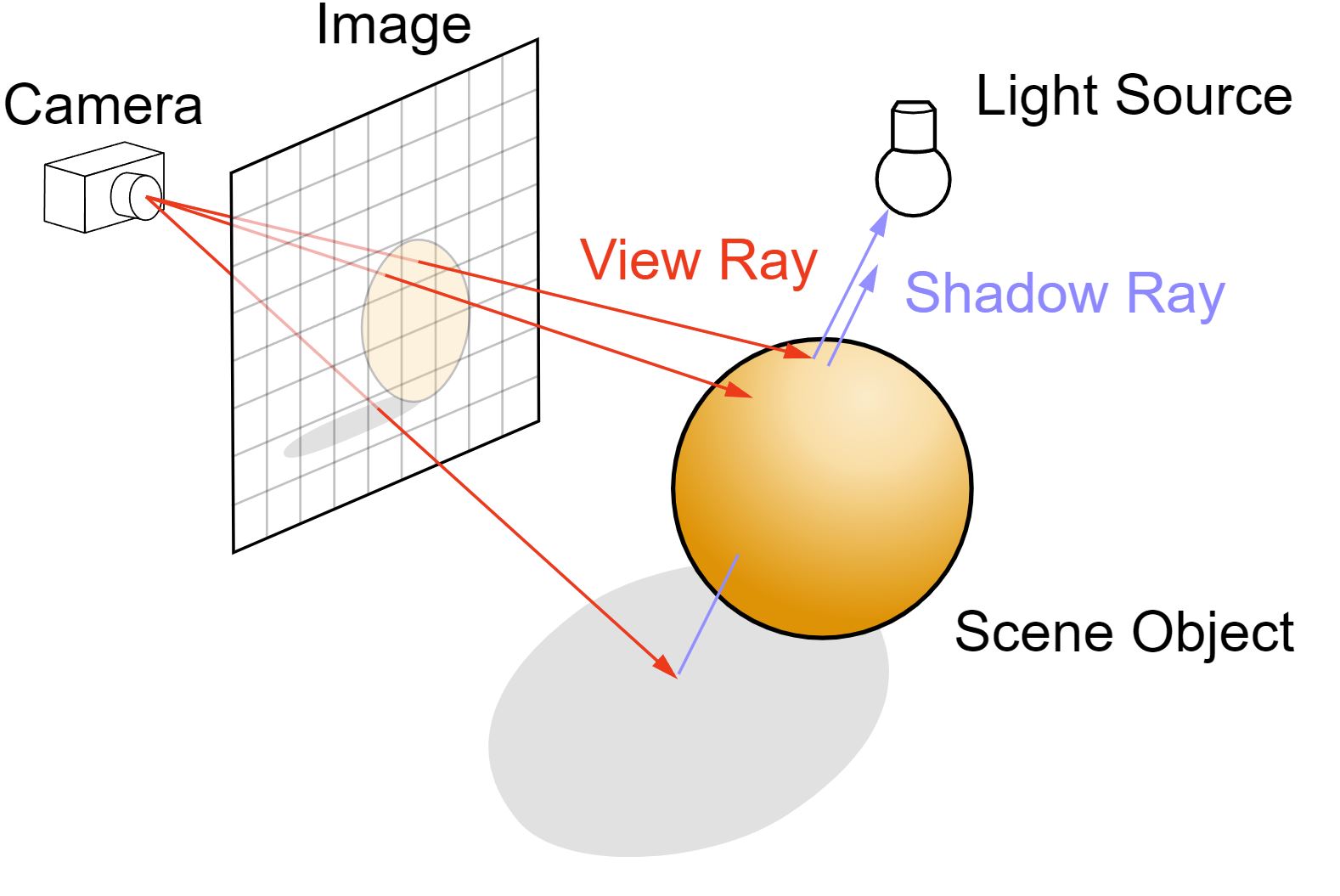
A ray tracer is software that allows the visualization of a 3D modeled scene based on the theory of inverse geometric optics. The objective is to launch rays from a point of observation (a camera) and follow the inverse optical path of this ray. When there is an intersection between the ray and an object in the environment, a shading calculation determines if the intersected object is illuminated by a light source and evaluates the color that it will reflect and transmit towards the point of observation.

scene
Figure 1. Ray tracing scene

1. The Equation of a Ray

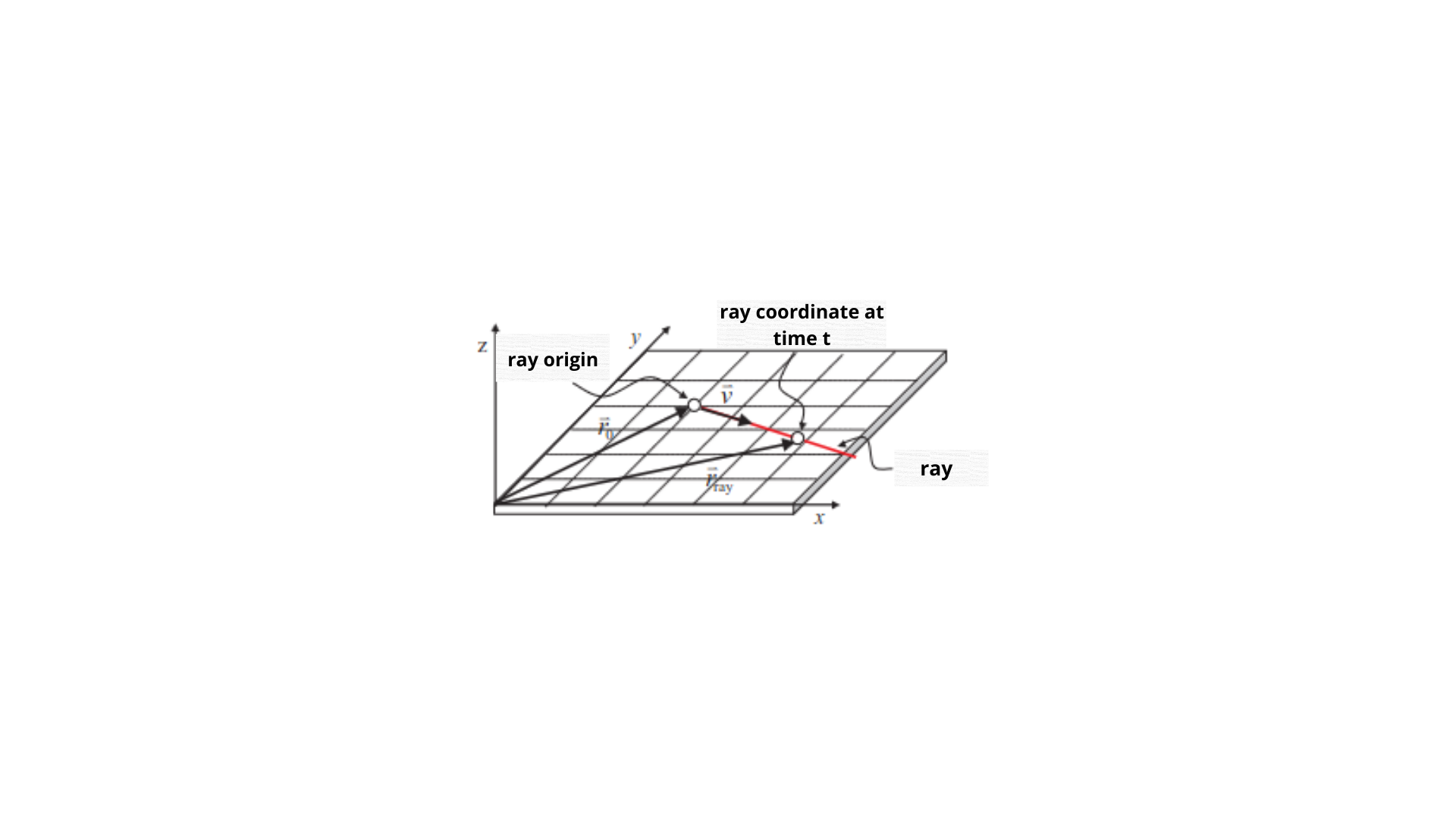
A ray $\vec{r}_{\text {my }}$ is a structure with an origin $\vec{r}_0$ and a direction $\vec{v}$. It allows for the calculation of intersections with geometric shapes in a scene. A time parameter $t$ is used to chronologically order the ray’s intersections with objects in the scene.

modeling
Figure 2. Ray equation at time t (see page 2)

A ray parameterized over time has the following form:

\[\vec{r}_{\text {ray }}=\vec{r}_0+\vec{v} t\]

where

$ \vec{r}_{\text {ray }}$ : Coordinate hit by the ray after a time $t$.

$\vec{r}_0:$ Origin of the ray.

$\bar{v}$ : Direction of the ray $(\|\bar{v}\|=1$, unit vector $)$.

$t$ : Time elapsed in the ray’s movement.

In computing, the definition of a ray will need the following variables:

Ray Geometry Information on the intersected geometry

Origin position of the ray (\(\bar{r}_0\))

Direction of the ray (\(\bar{v}\))

The time \(t\) to intercept the geometry.

The normal to the surface \(\bar{n}\) at the interception site.

A texture coordinate \(uv\) (if any).

Reference to the material applied on the geometry (e.g., to obtain the color of the geometry).

In this part of the code, we define the components of a ray

template <int RealDim>
class BVHRay
{
public:
   using vec_t = eigen_vector_type<RealDim>;
   BVHRay(vec_t const& orig, vec_t const& dir,
        double dmin = 0, double dmax = std::numeric_limits<double>::max() )
     :
     M_origin( orig ),
     M_dir( dir ),
     M_distanceMin( dmin ),
     M_distanceMax( dmax )
     {}
   BVHRay() : BVHRay(vec_t::Zero(),vec_t::Zero()) {}
   BVHRay( BVHRay const& ) = default;
   BVHRay( BVHRay &&) = default;
   BVHRay& operator=( BVHRay && ) = default;
   BVHRay& operator=( BVHRay const& ) = default;
   vec_t const& origin() const noexcept { return M_origin; }
   vec_t const& dir() const noexcept { return M_dir; }
   double distanceMin() const { return M_distanceMin; }
   double distanceMax() const { return M_distanceMax; }
private:
   friend class boost::serialization::access;
   template <class Archive>
    void serialize( Archive& ar, const unsigned int version )
     {
         ar & M_origin;
         ar & M_dir;
         ar & M_distanceMin;
         ar & M_distanceMax;
     }
private:
   vec_t M_origin, M_dir;  // ray origin and dir
   double M_distanceMin, M_distanceMax;
};

2. Ray-sphere intersection

  • Condition I:point is on ray

\[\mathbf{r}(t)=\mathbf{p}+t \mathbf{\vec{d}}\]

  • Condition 2: point is on sphere

  • Let be a sphere of radius r, the ray intersects the sphere so

\[\begin{aligned} & \|\mathbf{x}\|=r \Leftrightarrow\|\mathbf{x}\|^2=r^2 \\ & f(\mathbf{x})=\mathbf{x} \cdot \mathbf{x}-r^2=0 \end{aligned}\]

  • Substitute:

\[(\mathbf{p}+t \mathbf{\vec{d}}) \cdot(\mathbf{p}+t \mathbf{\vec{d}})-r^2=0\]

  • this is a quadratic equation in $t$

  • Solution for $t$ by quadratic formula:

\[t =\frac{-\mathbf{d} \cdot \mathbf{p} \pm \sqrt{(\mathbf{d} \cdot \mathbf{p})^2-(\mathbf{d} \cdot \mathbf{d})(\mathbf{p} \cdot \mathbf{p}-r^2)}}{\mathbf{d} \cdot \mathbf{d}} \\\]

  • simpler form holds when $\mathbf{d}$ is a unit vector.

\[t =-\mathbf{d} \cdot \mathbf{p} \pm \sqrt{(\mathbf{d} \cdot \mathbf{p})^2-\mathbf{p} \cdot \mathbf{p}+r^2}\]

For more explanation, see here.

In this method of template intersect we compute intersection with a ray from the BVH built and return a vector of intersection result

template<typename... Ts>
auto intersect( Ts && ... v )
    {
        auto args = NA::make_arguments( std::forward<Ts>(v)... );
        auto && ray = args.get(_ray);
        bool useRobustTraversal = args.get_else(_robust,true);
        IntersectContext ctx = args.get_else(_context,IntersectContext::closest);
        bool parallel = args.get_else(_parallel,this->worldComm().size() > 1);
        bool closestOnly = ctx == IntersectContext::closest;
        using napp_ray_type = std::decay_t<decltype(ray)>;
        if constexpr( std::is_same_v<BVHRaysDistributed<nRealDim>,napp_ray_type> ) // case rays distributed on process
        {
            // WARNING: this algo is not good (all_gather of rays then all run bvh), just a quick version for test
            auto const& localRays = ray.rays();
            std::vector<int> resLocalSize( this->worldComm().size() );
            mpi::all_gather( this->worldComm(), (int)localRays.size(), resLocalSize );
            std::vector<ray_type> raysGathered;
            if ( this->worldComm().isMasterRank() )
            {
                int gatherRaySize = std::accumulate( resLocalSize.begin(), resLocalSize.end(), 0 );
                raysGathered.resize( gatherRaySize );
            }
            mpi::gatherv( this->worldComm(), localRays, raysGathered.data(), resLocalSize, this->worldComm().masterRank() );
            mpi::broadcast( this->worldComm(), raysGathered, this->worldComm().masterRank() );
            auto intersectGlobal = this->intersect(_ray=raysGathered,_robust=useRobustTraversal,_context=ctx,_parallel=true);
            std::vector<std::vector<rayintersection_result_type>> res;
            res.resize( ray.numberOfLocalRay() );
            std::size_t startRayIndexInThisProcess = 0;
            for ( int p=0;p<this->worldComm().rank();++p )
                startRayIndexInThisProcess += resLocalSize[p];
            std::copy_n(intersectGlobal.cbegin()+startRayIndexInThisProcess, localRays.size(), res.begin());
            return res;
        }
        else if constexpr ( is_iterable_v<std::decay_t<decltype(ray)>> ) // case rays container are identical all on process (TODO: internal case)
        {
            std::vector<std::vector<rayintersection_result_type>> resSeq;
            resSeq.reserve( ray.size() );
            for ( auto const& currentRay : ray )
            {
                auto currentResSeq = this->intersectSequential( currentRay,useRobustTraversal );
                if ( closestOnly && currentResSeq.size() > 1 )
                    currentResSeq.resize(1);
                resSeq.push_back( std::move( currentResSeq ) );
            }
            if ( !parallel )
                return resSeq;
            mpi::all_reduce( this->worldComm(), mpi::inplace( resSeq ), [](auto const& x, auto const& y) -> std::vector<std::vector<rayintersection_result_type>> {
                    std::size_t retSize = x.size();
                    std::vector<std::vector<rayintersection_result_type>> ret;
                    DCHECK( x.size() == y.size() ) << "not same size x:" << x.size() << " y:" << y.size();
                    ret.reserve( retSize );
                    for ( int k = 0; k < retSize ; ++k )
                    {
                        auto const& a = x[k];
                        auto const& b = y[k];
                        if ( a.empty() )
                            ret.push_back( b );
                        else if ( b.empty() )
                            ret.push_back( a );
                        else
                        {
                            // WARNING only return one intersection (closest or anyhint)
                            if ( a.front().distance() < b.front().distance() )
                                ret.push_back( a );
                            else
                                ret.push_back( b );
                        }
                    }
                    return ret;
                } );
            return resSeq;
        }
        else // only one ray (all process should have the same ray if parallel=true)
        {
            auto resSeq = this->intersectSequential( ray,useRobustTraversal );
            if ( closestOnly && resSeq.size() > 1 )
                resSeq.resize(1);
            if ( !parallel )
                return resSeq;
        }
    }

Next: BVH



back to main page